搜索
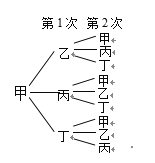
【题目】（1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．求第二次传球后球回到甲手里的概率．（请用“画树状图”的方式给出分析过程）
（2）如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是 （请直接写出结果）．
参考答案：
【答案】（1）
（2）
【解析】试题分析：（1）画树状图（或列表）求出第二次传球后所有结果，再找出第二次传球后球回到甲手里的结果，即可求得第二次传球后球回到甲手里的概率；（2）画树状图（或列表）求:当n=2时，第三次传球后所有结果有8种，第三次传球后球回到甲手里的结果有2种，所以第三次传球后球回到甲手里的概率是
；当n=3时，第三次传球后所有结果有27种，第三次传球后球回到甲手里的结果有6种，所以第三次传球后球回到甲手里的概率是
；依次类推，如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是
．
试题解析：（1）画树状图：
或：列表：
甲 | 乙 | 丙 | 丁 | |
乙 | 乙甲 | / | 乙丙 | 乙丁 |
丙 | 丙甲 | 丙乙 | / | 丙丁 |
丁 | 丁甲 | 丁乙 | 丁丙 | / |
共有9种等可能的结果，其中符合要求的结果有3种，
∴P（第2次传球后球回到甲手里）＝
＝
．
（2）
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：善于思考的小明在解方程组
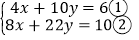时，采用了一种“整体代换”的解法，解法如下：解：将方程②8x+20y+2y=10，变形为 2（4x+10y）+2y=10③，把方程①代入③得，2×6+2y=10，则 y=﹣1；把 y=﹣1 代入①得，x=4，所以方程组的解为：
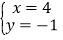请你解决以下问题：（1）试用小明的“整体代换”的方法解方程组
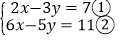
（2）已知 x、y、z，满足
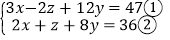试求 z 的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△ABD都是⊙O的内接三角形，圆心O在边AB上，边AD分别与BC，OC交于E，F两点，点C为
的中点．(1)求证：OF∥BD；
(2)若点F为线段OC的中点，且⊙O的半径R＝6 cm，求图中阴影部分(弓形)的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝－2x与直线y＝kx＋b相交于点A(a,2)，并且直线y＝kx＋b经过x轴上点B(2,0)．
(1)求直线y＝kx＋b的解析式；
(2)求两条直线与y轴围成的三角形面积；
(3)直接写出不等式(k＋2)x＋b≥0的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润
与投资量
成正比例关系，如图（1）所示；种植花卉的利润
与投资量
成二次函数关系，如图（2）所示（注：利润与投资量的单位：万元）
（1）分别求出利润
与关于投资量的函数关系式；（2）如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场试销一种成本价为每件60元的服装，规定试销期间销售单价不低于成本单价，获利不得高于40%．经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=80时，y=40；x=70时，y=50．
（1）求一次函数y=kx+b的表达式；
（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程a2x2+（2a－1）x+1=0有两个不相等的实数根x1，x2．（1）求a的取值范围；（2）是否存在实数a，使方程的两个实数根互为相反数？如果存在，求出a的值；如果不存在，说明理由．
解：（1）根据题意，得△=（2a－1）2－4a2>0，解得a<
．∴当a<0时，方程有两个不相等的实数根．
（2）存在，如果方程的两个实数根x1，x2互为相反数，则x1+x2=－
=0 ①，解得a=
，经检验，a=
是方程①的根．∴当a=
时，方程的两个实数根x1与x2互为相反数．上述解答过程是否有错误？如果有，请指出错误之处，并解答．
相关试题
