搜索
【题目】如图，根据图形填空：
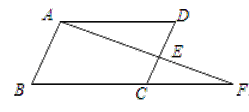
已知：∠DAF＝∠F，∠B＝∠D，AB与DC平行吗？
解：∠DAF＝∠F （ ）
∴AD∥BF（ ），
∴∠D＝∠DCF（ ）
∵∠B＝∠D （ ）
∴∠B＝∠DCF （ ）
∴AB∥DC（ ）
参考答案：
【答案】见解析.
【解析】
首先根据已知，应用内错角相等，两直线平行，证得AD∥BF；利用两直线平行，内错角相等，证得∠D＝∠DCF，又由已知，利用等量代换，证得∠B＝∠DCF，根据同位角相等，两直线平行，证得AB∥DC．
解：∠DAF＝∠F （ 已知），
∴AD∥BF（ 内错角相等，两直线平行），
∴∠D＝∠DCF（ 两直线平行，内错角相等），
∵∠B＝∠D （ 已知），
∴∠B＝∠DCF （ 等量代换），
∴AB∥DC（ 同位角相等，两直线平行）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，二次函数y=mx2﹣（2m+1）x+m﹣5的图象与x轴有两个公共点．
（1）求m的取值范围；
（2）若m取满足条件的最小的整数， ①写出这个二次函数的解析式；
②当n≤x≤1时，函数值y的取值范围是﹣6≤y≤4﹣n，求n的值；
③将此二次函数平移，使平移后的图象经过原点O．设平移后的图象对应的函数表达式为y=a（x﹣h）2+k，当x＜2时，y随x的增大而减小，求k的取值范围． -
科目： 来源： 题型：
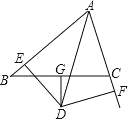
查看答案和解析>>【题目】如图，G 为 BC 的中点，且 DG⊥BC，DE⊥AB 于 E，DF⊥AC 于 F， BE＝CF．
（1）求证：AD 是∠BAC 的平分线；
（2）如果 AB＝8，AC＝6，求 AE 的长．
-
科目： 来源： 题型：
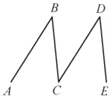
查看答案和解析>>【题目】如图，如果AB∥CD，∠B＝37°，∠D＝37°，那么BC与DE平行吗？完成下面解答过中的填空或填写理由．
解：∵AB∥CD （ 已知），
∴∠B＝ （ ）
∵∠B＝∠D＝37°（已知）
∴ ＝∠D （等量代换）
∴BC∥DE （ ）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=BC，BD⊥AC于点D．
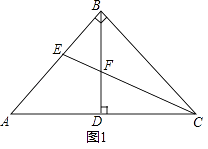
（1）如图1，当∠ABC=90°时，若CE平分∠ACB，交AB于点E，交BD于点F． ①求证：△BEF是等腰三角形；
②求证：BD=
（BC+BF）；
（2）点E在AB边上，连接CE．若BD= （BC+BE），在图2中补全图形，判断∠ACE与∠ABC之间的数量关系，写出你的结论，并写出求解∠ACE与∠ABC关系的思路．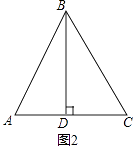 
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，若点P和点P1关于y轴对称，点P1和点P2关于直线l对称，则称点P2是点P关于y轴，直线l的二次对称点．
（1）如图1，点A（﹣1，0）．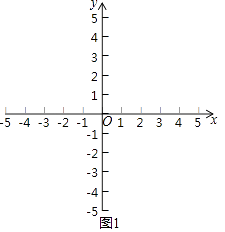
①若点B是点A关于y轴，直线l1：x=2的二次对称点，则点B的坐标为；
②若点C（﹣5，0）是点A关于y轴，直线l2：x=a的二次对称点，则a的值为；
③若点D（2，1）是点A关于y轴，直线l3的二次对称点，则直线l3的表达式为；
（2）如图2，⊙O的半径为1．若⊙O上存在点M，使得点M'是点M关于y轴，直线l4：x=b的二次对称点，且点M'在射线y=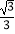
x（x≥0）上，b的取值范围是；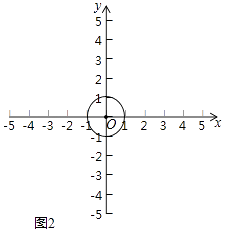 
（3）E（t，0）是x轴上的动点，⊙E的半径为2，若⊙E上存在点N，使得点N'是点N关于y轴，直线l5：y=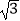
x+1的二次对称点，且点N'在y轴上，求t的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在 Rt△ABC 中，∠C＝90°，∠A＝60°，AB＝10cm，若点M 从点 B 出发以 2cm/s 的速度向点 A 运动，点 N 从点 A 出发以 1cm/s 的速度向点 C 运动，设 M、N 分别从点 B、A 同时出发，运动的时间为 ts．
（1）用含 t 的式子表示线段 AM、AN 的长；
（2）当 t 为何值时，△AMN 是以 MN 为底边的等腰三角形？
（3）当 t 为何值时，MN∥BC？并求出此时 CN 的长．
相关试题
