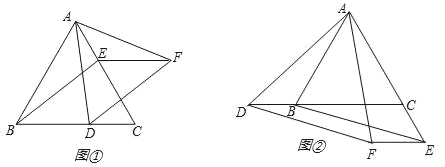
【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.
参考答案:
【答案】(1)证明见解析(2)△ADF是等边三角形(3)△ADF仍是等边三角形
【解析】
(1)△ABE、△CAD中,已知的条件有:AB=AC,∠BAE=∠ACD=60°;若求两个三角形全等,只需再证得AE=CD即可,易知AC=BC,而BD=CE,即可得到AE=CD,由此得证;
(2)易证得四边形BDFE是平行四边形,则BE=DF=AD;设AD、BE交于G,则∠ADF=∠BGD;
而∠BGD=∠ABE+∠DAB,由(1)的全等三角形知:∠DAC=∠ABE,故∠BGD=∠DAC+∠DAB=60°,等量代换后,可求得∠ADF=60°,即可得到△ADF是等边三角形的结论.
(3)与(2)的结论相同,解题思路与(1)(2)完全相同.
(1)证明:∵△ABC是等边三角形,
∴∠BAE=∠C=60°,AB=AC=BC;
∵BD=CE,
∴AC﹣CE=BC﹣BD,∴AE=CD;
又AB=AC,
∴△ABE≌△CAD;
(2)△ADF是等边三角形,理由如下:
∵△ABC是等边三角形,∴∠BAC=60°;
∵DF∥BE,EF∥BC,
∴∠1=∠2,四边形BDFE是平行四边形;
∴BE=DF;
∵△ABE≌△CAD,∴∠4=∠5,BE=AD,∴DF=AD;
∵∠1=∠3+∠4,∴∠2=∠3+∠5=∠BAC=60°;
∴△ADF是等边三角形;
(3)△ADF仍是等边三角形,理由如下:
∵△ABC是等边三角形,∴∠ABC=∠BAE=∠C=60°,AB=BC;
∴∠ABD=∠BCD=180°﹣120°;
∵BD=CE,∴△ABD≌△BCE,∴∠1=∠3,BE=AD;
∵DF∥BE,EF∥BC,
∴∠1=∠2,四边形BDFE是平行四边形;
∴BE=DF,∴DF=AD;
∵∠3+∠4=∠ABC=60°,∴∠2+∠4=60°即∠ADF=60°
∴△ADF是等边三角形.
-
科目: 来源: 题型:
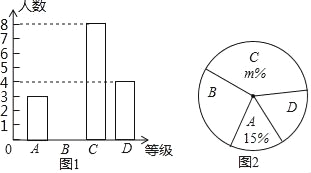
查看答案和解析>>【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为 ,表示“D等级”的扇形的圆心角为 度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
-
科目: 来源: 题型:
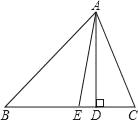
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,AE为∠BAC的平分线,且∠B=36°,∠C=66°.求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
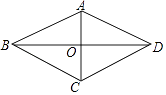
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2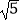 ,求四边形ABCD的面积.
,求四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
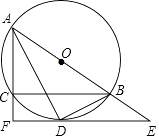
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
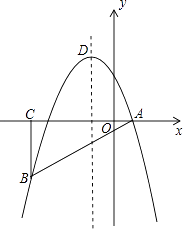
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
相关试题

