【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.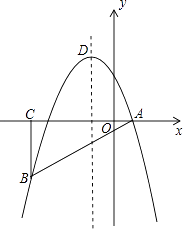
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵A,C的坐标分别为(1,0),(﹣4,0),
∴AC=5.
∵△ABC为等腰直角三角形,∠C=90°,
∴BC=AC=5.
∴B(﹣4,﹣5).
将点A和点B的坐标代入得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+3.
(2)解:如图1所示:
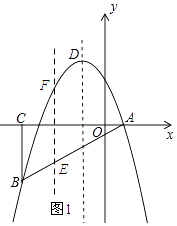
设直线AB的解析式为y=kx+b,将点A和点B的坐标代入得: ![]() ,解得:k=1,b=﹣1.
,解得:k=1,b=﹣1.
所以直线AB的解析式为y=x﹣1.
设点E的坐标为(t,t﹣1),则点F的坐标为(t,﹣t2﹣2t+3).
∴EF=﹣t2﹣2t+3﹣(t﹣1)=﹣t2﹣3t+4=(t+ ![]() )2+
)2+ ![]() .
.
∴当t=﹣ ![]() 时,FE取最大值
时,FE取最大值 ![]() ,此时,点E的坐标为(﹣
,此时,点E的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).
).
(3)解:存在点P,能使△PEF是以EF为直角边的直角三角形.
理由:如图所示:过点F作直线a⊥EF,交抛物线于点P,过点E作直线b⊥EF,交抛物线P′、P″.
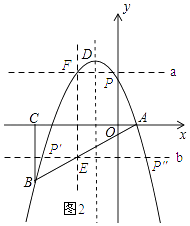
由(2)可知点E的坐标为(t,t﹣1),则点F的坐标为(t,﹣t2﹣2t+3),t=﹣ ![]() ,
,
∴点E(﹣ ![]() ,﹣
,﹣ ![]() )、F(﹣
)、F(﹣ ![]() ,
, ![]() ).
).
①当﹣t2﹣2t+3= ![]() 时,解得:x=﹣
时,解得:x=﹣ ![]() 或x=﹣
或x=﹣ ![]() (舍去).
(舍去).
∴点P的坐标为(﹣ ![]() ,
, ![]() ).
).
②当﹣t2﹣2t+3=﹣ ![]() 时,解得:x=﹣1+
时,解得:x=﹣1+ ![]() 或x=﹣1﹣
或x=﹣1﹣ ![]() .
.
∴点P′(﹣1﹣ ![]() ,﹣
,﹣ ![]() ),P″(﹣1+
),P″(﹣1+ ![]() ,﹣
,﹣ ![]() ).
).
综上所述,点P的坐标为(﹣ ![]() ,
, ![]() )或(﹣1﹣
)或(﹣1﹣ ![]() ,﹣
,﹣ ![]() )或P″(﹣1+
)或P″(﹣1+ ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)要求解析式关键在于求B点坐标,由△ABC为等腰直角三角形,∠C=90°,BC=AC=5.可求出B(﹣4,﹣5),把A、B坐标代入解析式即可;(2)求最值问题可化归为函数最值问题,因此须构建以E点横坐标t为自变量、EF长度为因变量的函数,用t的代数式表示EF,EF是竖直线段,其长度可用上端点纵坐标减下端点纵坐标,构建函数后,若是二次函数可用配方法求出最值;(3)以EF为直角边的直角三角形可分为两类:以E为直角顶点;以F为直角顶点;因此须过E、F分别作EF的垂线 与抛物线的交点就是P点.
-
科目: 来源: 题型:
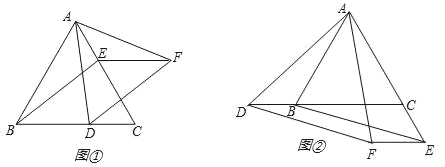
查看答案和解析>>【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
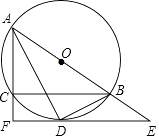
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
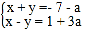 的解x为非正数,y为负数.
的解x为非正数,y为负数.(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣x+1(0≤x≤10)与反比例函数y=
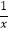 (﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )
(﹣10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1 , y1),(x2 , y2)是图象上两个不同的点,若y1=y2 , 则x1+x2的取值范围是( )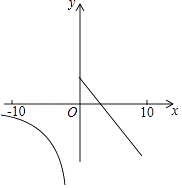
A.﹣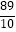 ≤x≤1
≤x≤1
B.﹣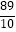 ≤x≤
≤x≤ 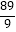
C.﹣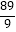 ≤x≤
≤x≤ 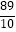
D.1≤x≤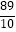
-
科目: 来源: 题型:
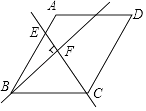
查看答案和解析>>【题目】如图,在菱形ABCD中,∠ABC=60°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A.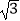
B.2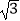
C. π
π
D. π
π
相关试题

