【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.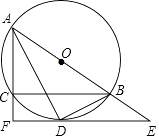
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
参考答案:
【答案】
(1)证明:
如图1,连接OD,
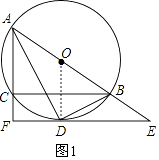
∵EF是⊙O的切线,且点D在⊙O上,
∴OD⊥EF,
∵OA=OD,
∴∠DAB=∠ADO,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∴∠ADO=∠DAC,
∴AF∥OD,
∴AF⊥EF;
(2)解:
如图2,过D作DG⊥AE于点G,连接CD,
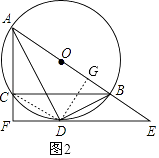
∵∠BAD=∠DAF,AF⊥EF,DG⊥AE,
∴BD=CD,DG=DF,
在Rt△ADF和Rt△ADG中
![]()
∴Rt△ADF≌Rt△ADG(HL),
同理可得Rt△CDF≌Rt△BDG,
∴BG=CF=2,AG=AF=AC+CF=6+2=8,
∴AB=AG+BG=8+2=10,
∴⊙O的半径OA= ![]() AB=5.
AB=5.
【解析】(1)本题主要考查切线的性质及圆周角定理,连接OD,由切线的性质和已知条件可证得OD∥EF,再由平行线的判定则可证得所求的答案;
(2)通过过D作DG⊥AE于点G,连接CD,则可证得△ADF≌△ADG、△CDF≌△BDG,由三角形全等则可求得AB的长,再可求得圆的半径即可.
-
科目: 来源: 题型:
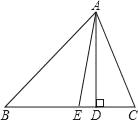
查看答案和解析>>【题目】如图,已知△ABC中,AD⊥BC于点D,AE为∠BAC的平分线,且∠B=36°,∠C=66°.求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,BD平分∠ABC,AC⊥BD,垂足为点O.
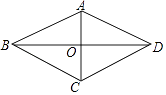
(1)求证:四边形ABCD是菱形;
(2)若CD=3,BD=2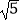 ,求四边形ABCD的面积.
,求四边形ABCD的面积. -
科目: 来源: 题型:
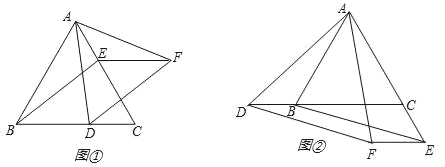
查看答案和解析>>【题目】如图①,△ABC是等边三角形,D、E分别为边BC和AC上的点,且BD=CE,过D作BE的平行线,过E作BC的平行线,它们交于点F,连接AF.
(1)求证:△ABE≌△CAD;
(2)试判断△ADF的形状,并说明理由;
(3)若将D、E分别移为边CB的延长线和AC的延长线上的点,其它条件不变(如图②),则△ADF的形状是否改变,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=﹣x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
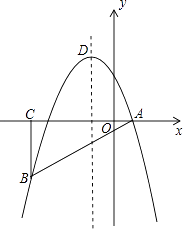
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
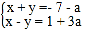 的解x为非正数,y为负数.
的解x为非正数,y为负数.(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3)在a的取值范围内,m是最大的整数,n是最小的整数,求(m+n)m-n的值;
(4)在a的取值范围内,当a取何整数时,不等式2ax+x>2a+1的解为x<1.
相关试题

