【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长.
参考答案:
【答案】
(1)
证明:连接EC.
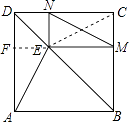
∵四边形ABCD是正方形,EM⊥BC,EN⊥CD,
∴∠NCM=∠CME=∠CNE=90°,
∴四边形EMCN为矩形.
∴MN=CE.
又∵BD为正方形ABCD的对角线,
∴∠ABE=∠CBE.
在△ABE和△CBE中
∵ 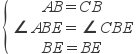 ,
,
∴△ABE≌△CBE(SAS).
∴AE=EC.
∴AE=MN.
(2)
解:过点E作EF⊥AD于点F,
∵AE=2,∠DAE=30°,
∴EF= ![]() AE=1,AF=AEcos30°=2×
AE=1,AF=AEcos30°=2× ![]() =
= ![]() .
.
∵BD是正方形ABCD的对角线,
∴∠EDF=45°,
∴DF=EF=1,
∴AD=AF+DF= ![]() +1,即正方形的边长为
+1,即正方形的边长为 ![]() +1.
+1.
【解析】(1)连接EC,根据题意可得出四边形EMCN为矩形,故MN=CE,再由SAS定理得出△ABE≌△CBE,进而可得出结论;(2)过点E作EF⊥AD,由直角三角形的性质可得出EF及AF的长,再由等腰直角三角形的性质得出DF的长,进而可得出结论.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距聚会还有42分钟,于是分立即步行(匀速)回家,在家拿道具用了1分钟,然后骑自行车(匀速)返回学校,已知李明骑自行车的速度是步行速度的3倍,李明骑自行车到学校比他从学校步行到家少用了20分钟.
(1)李明步行的速度是多少米/分?
(2)李明能否在联欢会开始前赶到学校? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,回答问题:
(1)在化简 的过程中,小张和小李的化简结果不同;
的过程中,小张和小李的化简结果不同;
小张的化简如下: =
=  =
=  =
=  ﹣
﹣ 
小李的化简如下: =
=  =
=  =
=  ﹣
﹣ 
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)请你利用上面所学的方法化简 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】 下列运算中,正确的是( )
A. a6÷a3=a2B. (﹣a+b)(﹣a﹣b)=b2﹣a2
C. 2a+3b=5abD. ﹣a(2﹣a)=a2﹣2a
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分) 已知双曲线y=
 (x>0),直线l1:y﹣
(x>0),直线l1:y﹣ =k(x﹣
=k(x﹣ )(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+
)(k<0)过定点F且与双曲线交于A,B两点,设A(x1,y1),B(x2,y2)(x1<x2),直线l2:y=﹣x+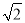 .
.(1)若k =﹣1,求△OAB的面积S;
(2)若AB=
 ,求k的值;
,求k的值;(3)设N(0,2
 ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形,若存在,请求出Q点的坐标。
),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形,若存在,请求出Q点的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:12﹣(﹣18)+(﹣7)﹣15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2a2)3正确的是( )
A. 8a5B. ﹣6a6C. ﹣8a5D. ﹣8a6
相关试题

