【题目】如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。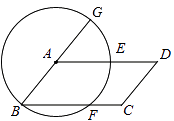
参考答案:
【答案】解:相等.
理由:连接AF.
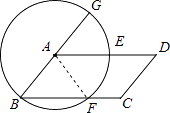
∵A为圆心,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠AFB=∠DAF,∠GAD=∠ABF,
∴∠DAF=∠GAD,
∴ ![]() .
.
【解析】要证弧EF和弧FG相等,就需证这两条弧所对的圆心角相等。因此连接AF,根据已知的平行四边形得到AD∥BC,证明∠AFB=∠DAF,∠GAD=∠ABF,再根据等腰三角形的性质证明∠ABF=∠AFB,就可得出∠DAF=∠GAD,即可证得结论。
【考点精析】本题主要考查了平行线的性质和平行四边形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
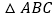 中,已知
中,已知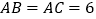 ,
,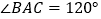 ,
, ,点
,点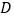 是
是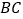 边上的任意一动点,点
边上的任意一动点,点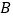 与点
与点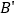 关于直线
关于直线 对称,直线
对称,直线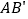 与直线
与直线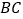 相交于点
相交于点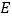 .
. (1)求
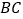 边上的高;
边上的高;(2)当
 为何值时,△
为何值时,△ 与△
与△ 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;(3)连接
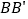 ,当
,当 为直角三角形时,求
为直角三角形时,求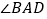 的度数.
的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
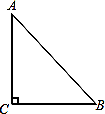
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)(﹣1)2018+3﹣2﹣(π﹣3.14)0
(2)(x+3)2﹣x2
(3)(x+2)(3x﹣y)﹣3x(x+y)
(4)(2x+y+1)(2x+y﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
解: ,理由如下:
∵AB∥CD,
∴∠B=∠BCD,( )
∵∠B=70°,
∴∠BCD=70°,( )
∵∠BCE=20°,
∴∠ECD=50°,
∵∠CEF=130°,
∴ + =180°,
∴EF∥ ,( )
∴AB∥EF.( )

-
科目: 来源: 题型:
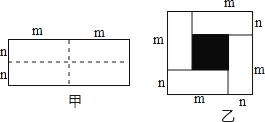
查看答案和解析>>【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均剪成四个小长方形,然后拼成如图乙所示的一个大正方形.
(1)你认为图乙中的阴影部分的正方形的边长= ;
(2)请用两种不同的方法求图乙中阴影部分的面积:
方法一:
方法二:
(3)观察图乙,请你写出下列代数式之间的等量关系:
(m+n)2、(m﹣n)2、mn
.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=7,求a﹣b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
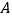 在数轴上表示的数是-8,点
在数轴上表示的数是-8,点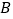 在数轴上表示的数是16.若点
在数轴上表示的数是16.若点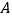 以6个单位长度/秒的速度向右匀速运动,同时点
以6个单位长度/秒的速度向右匀速运动,同时点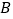 以2个单位长度/秒的速度向左匀速运动.问:当
以2个单位长度/秒的速度向左匀速运动.问:当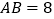 时,运动时间为多少秒?
时,运动时间为多少秒?
A. 2秒B. 13.4秒C. 2秒或4秒D. 2秒或6秒
相关试题

