【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



参考答案:
【答案】(1)3(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)过点A做AP![]() BC垂足为P,根据题意推出
BC垂足为P,根据题意推出![]() B=
B=![]() C=30
C=30![]() ,再求出AP的值即为BC边上的高;
,再求出AP的值即为BC边上的高;
(2)由对称及AD与DC至少有一段不会超过BC的一半,得出当△ADB![]() 与△ADC完全重合时,即当BD=3
与△ADC完全重合时,即当BD=3![]() 时△ADB
时△ADB![]() 与△ADC重叠部分的面积最大;
与△ADC重叠部分的面积最大;
(3)先判断只有![]() BDB
BDB![]() =90
=90![]() 才符合题意,再分别讨论当点
才符合题意,再分别讨论当点![]() 在点
在点![]() 右侧时或右侧时即可.
右侧时或右侧时即可.
(1)过点![]() 做
做![]() 垂足为
垂足为![]()
∵![]() 且
且![]()
∴![]()
在![]() 中
中![]() ,
,![]()
∴![]()
∴底边![]() 上的高
上的高![]() .
.

(2)当![]() 时,△
时,△![]() 与△
与△![]() 重叠部分的面积最大.
重叠部分的面积最大.
此时![]() 、
、![]() 、
、![]() 三点重合,重叠部分为△
三点重合,重叠部分为△![]() ,其面积为:
,其面积为:
![]()
(理由如下:∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,∴△
对称,∴△![]() 与△
与△![]() 关于直线
关于直线![]() 对称,∴△
对称,∴△![]() ≌△
≌△![]() ,∴
,∴![]() ,∵
,∵![]() 与
与![]() 至少有一段不会超过
至少有一段不会超过![]() 的一半,∴
的一半,∴![]() 与
与![]() 至少有一个不会超过
至少有一个不会超过![]() 的一半,∴
的一半,∴![]() 与
与![]() 至少有一个不会超过
至少有一个不会超过![]() 的一半,∴当△
的一半,∴当△![]() 与△
与△![]() 完全重合时,△
完全重合时,△![]() 与△
与△![]() 重叠部分的面积最大,并且最大值为
重叠部分的面积最大,并且最大值为![]() 的一半).
的一半).
(3)由轴对称可知:![]() ,∴
,∴![]()
即当![]() 为直角三角形时,
为直角三角形时,

![]() .
.
如图:当点![]() 在点
在点![]() 右侧时
右侧时
由轴对称可知:![]()
∴.![]()
![]()
![]()
∴![]()
![]()
![]() .
.

如图:当点![]() 在点
在点![]() 左侧时
左侧时
由轴对称可知:![]() .
.
![]()
![]()
∴![]()
![]()
![]()
综上所述,当![]() 为直角三角形时,
为直角三角形时,![]() 的度数为
的度数为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与思考:
整式乘法与因式分解是方向相反的变形,由

 ,
,可得
 .
.利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子
 分解因式.
分解因式.这个式子的常数项
 ,一次项系
,一次项系 ,
,所以
 .
.
解:

 .
.上述分解因式
 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图). 请仿照上面的方法,解答下列问题:
(1)分解因式:
 =___________________;
=___________________;(2)若
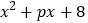 可分解为两个一次因式的积,则整数P的所有可能值是________.
可分解为两个一次因式的积,则整数P的所有可能值是________. -
科目: 来源: 题型:
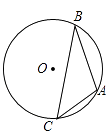
查看答案和解析>>【题目】已知:如图,A、B、C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“有趣三角形”,这条中线称为“有趣中线”。如图,在三角形ABC中,∠C=90°,较短的一条直角边BC=1,且三角形ABC是“有趣三角形”,求三角形ABC的“有趣中线”的长。
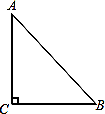
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题:
(1)(﹣1)2018+3﹣2﹣(π﹣3.14)0
(2)(x+3)2﹣x2
(3)(x+2)(3x﹣y)﹣3x(x+y)
(4)(2x+y+1)(2x+y﹣1)
-
科目: 来源: 题型:
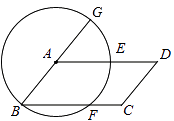
查看答案和解析>>【题目】如图所示,以平行四边形ABCD的顶点A为圆心,AB为半径作圆,分别交BC,AD于E,F两点,交BA的延长于G,判断弧EF和弧FG是否相等,并说明理由。
相关试题

