搜索
【题目】如图，点
在数轴上表示的数是-8，点
在数轴上表示的数是16．若点以6个单位长度/秒的速度向右匀速运动，同时点以2个单位长度/秒的速度向左匀速运动．问：当
时，运动时间为多少秒？
A. 2秒B. 13.4秒C. 2秒或4秒D. 2秒或6秒
参考答案：
【答案】C
【解析】
分点B在右边，点A在左边和点B在左边，点A在右边两种可能．用t表示AB的长度，根据AB=8列方程求解即可．
设当
时，运动时间为t秒，
根据题意A、B对应数字分别是：-8+6t和16-2t，
当点B在右边，点A在左边时，AB =16-2t-（-8+6t）=24-8t，
∵AB=8，∴24-8t＝8，∴t=2
当点B在左边，点A在右边时，AB =-8+6t -（16-2t）=-24+8t，
∵AB=8，∴-24+8t=8，∴t=4，
∴当时，运动时间为2秒或4秒
故选：C．
-
科目： 来源： 题型：
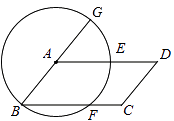
查看答案和解析>>【题目】如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，分别交BC，AD于E，F两点，交BA的延长于G，判断弧EF和弧FG是否相等，并说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，AB∥CD，∠B＝70°，∠BCE＝20°，∠CEF＝130°，请判断AB与EF的位置关系，并说明理由．
解： ，理由如下：
∵AB∥CD，
∴∠B＝∠BCD，（ ）
∵∠B＝70°，
∴∠BCD＝70°，（ ）
∵∠BCE＝20°，
∴∠ECD＝50°，
∵∠CEF＝130°，
∴ + ＝180°，
∴EF∥ ，（ ）
∴AB∥EF．（ ）
-
科目： 来源： 题型：
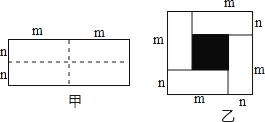
查看答案和解析>>【题目】已知图甲是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均剪成四个小长方形，然后拼成如图乙所示的一个大正方形．
（1）你认为图乙中的阴影部分的正方形的边长＝ ；
（2）请用两种不同的方法求图乙中阴影部分的面积：
方法一：
方法二：
（3）观察图乙，请你写出下列代数式之间的等量关系：
（m+n）2、（m﹣n）2、mn
．
（4）根据（3）题中的等量关系，解决如下问题：若a+b＝8，ab＝7，求a﹣b的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】八年级一班小张陪妈妈到水果市场购买水果，在一个水果摊前听到妈妈与售货员的对话：
妈妈：“售货员同志，请帮我买些上次梨.”
售货员：“大妈，您上次买的那种梨都卖完了，我们还没来得及进货，我建议这次您买些新进的苹果，价格比梨贵一点，不过苹果的营养价值更高.”
妈妈：“好，你们的服务态度和服务质量我很满意，这次我照上次一样，也买30元钱的苹果吧.”回家后对照前后两次的电脑小票，小张发现：每千克苹果的单价价是梨的单价的1.5倍，苹果的重量比梨轻2.5千克.
小张根据上面的对话和发票，求出了梨和苹果的单价，你知道梨和苹果的单价各是多少？
-
科目： 来源： 题型：
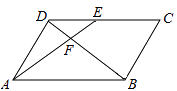
查看答案和解析>>【题目】如图，在平行四边形ABCD中，E为CD上一点，连结AE，BD，且AE，BD交于点F，S△DEF∶S△ABF=4∶25，求DE∶EC的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某一工程招标时，接到甲．乙两工程队的投标书，每施工一天，需付甲工程队工程款1.5万元，乙工程队工程款1.1万元．目前有三种施工方案：
方案一：甲队单独完成此项工程刚好如期完成；
方案二：乙队单独完成此项工程比规定日期多5天；
方案三：若甲．乙两队合作4天，剩下的工程由乙队单独做也正好如期完成．
哪一种方案既能如期完工又最节省工程款？
相关试题
