【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

参考答案:
【答案】(1)DM⊥EM,DM=EM,理由见解析; (2)DM⊥EM,DM=EM,理由见解析;(3)满足条件的MF的值为![]() 或
或![]() .
.
【解析】(1)结论:DM⊥EM,DM=EM.只要证明△AMH≌△FME,推出MH=ME,AH=EF=EC,推出DH=DE,因为∠EDH=90°,可得DM⊥EM,DM=ME;
(2)结论不变,证明方法同(1)类似;
(3)分两种情形画出图形,利用勾股定理以及等腰直角三角形的性质解决问题即可.
(1)结论:DM⊥EM,DM=EM,
理由:如图1中,延长EM交AD于H,
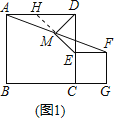
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME;
(2)如图2中,结论不变.DM⊥EM,DM=EM,
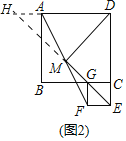
理由:如图2中,延长EM交DA的延长线于H,
∵四边形ABCD是正方形,四边形EFGC是正方形,
∴∠ADE=∠DEF=90°,AD=CD,
∴AD∥EF,
∴∠MAH=∠MFE,
∵AM=MF,∠AMH=∠FME,
∴△AMH≌△FME,
∴MH=ME,AH=EF=EC,
∴DH=DE,
∵∠EDH=90°,
∴DM⊥EM,DM=ME;
(3)如图3中,作MR⊥DE于R,
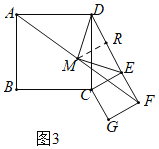
在Rt△CDE中,DE=![]() =12,
=12,
∵DM=NE,DM⊥ME,
∴MR=⊥DE,MR=![]() DE=6,DR=RE=6,
DE=6,DR=RE=6,
在Rt△FMR中,FM=![]() ,
,
如图4中,作MR⊥DE于R,

在Rt△MRF中,FM=![]() ,
,
故满足条件的MF的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
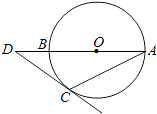
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20°
B.30°
C.40°
D.50° -
科目: 来源: 题型:
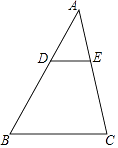
查看答案和解析>>【题目】如图,D,E分别是△ABC的边AB,AC上的点,且DE∥BC,AD=2,DB=3,△ADE的面是2,则四边形BCED的面积是( )
A.4
B.8
C.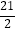
D.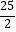
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题背景)
(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D
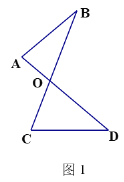
(简单应用)
(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=28°,∠ADC=20°,求∠P的度数(可直接使用问题(1)中的结论)
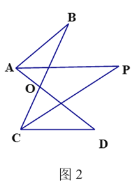
(问题探究)
(3)如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,若∠A=30°,∠C=18°,则∠P的度数为
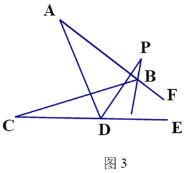
(拓展延伸)
(4)在图4中,若设∠C=x,∠B=y,∠CAP=
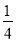 ∠CAB,∠CDP=
∠CAB,∠CDP=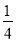 ∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)
∠CDB,试问∠P与∠C、∠B之间的数量关系为 (用x、y表示∠P)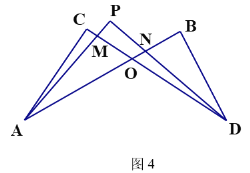
(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论 .
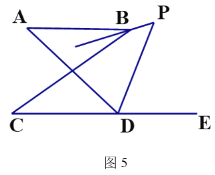
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.
求证:DE=BF.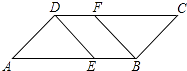
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲是一个大长方形剪去一个小长方形后形成的图形,已知动点 P 以每秒 2cm 的速度沿图甲的边框按从 B→C→D→E→F→A 的路径移动,相应的△ABP 的面积 S 与时间 t 之间 的关系如图乙中的图象表示.若 AB=6cm,则 b=_______.
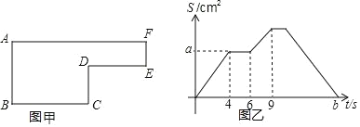
-
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”儿童节,某玩具超市设立了一个可以自由转动且只有铅笔和文具盒两个版块的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
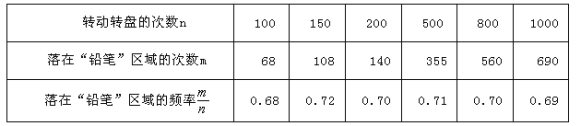

A.当
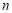 很大时,估计指针落在“铅笔”区域的频率大约是0.70
很大时,估计指针落在“铅笔”区域的频率大约是0.70 B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
相关试题

