【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合)使得
可以重合)使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对平衡点.
的一对平衡点.
(1)如图1,已知点![]() ,
,![]() ;
;
①设点![]() 与线段
与线段![]() 上一点的距离为
上一点的距离为![]() ,则
,则![]() 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是线段
是线段![]() 的一对平衡点的是 ;
的一对平衡点的是 ;
(2)如图2,已知![]() 的半径为1,点
的半径为1,点![]() 的坐标为
的坐标为![]() 在第一象限,且点
在第一象限,且点![]() 与点
与点![]() 是
是![]() 的一对平衡点,求
的一对平衡点,求![]() 的取值范围;
的取值范围;
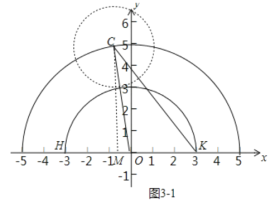
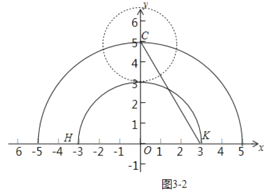
(3)如图3,已知点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 的正半轴于点
的正半轴于点![]() .点
.点![]() (其中
(其中![]() )是坐标平面内一个动点,且
)是坐标平面内一个动点,且![]() ,
,![]() 是以点
是以点![]() 为圆心,半径为2的圆,若
为圆心,半径为2的圆,若![]() 上的任意两个点都是
上的任意两个点都是![]() 的一对平衡点,直接写出
的一对平衡点,直接写出![]() 的取值范围.
的取值范围.



参考答案:
【答案】(1)①3,![]() ;②
;②![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①观察图象d的最小值是OA长,最大值是OB长,由勾股定理得出结果;②由题意知P1;
(2)如图,可得OE1=3,解得此时x=![]() ,OE2=7,解得x=3
,OE2=7,解得x=3![]() ,可求出范围;
,可求出范围;
(3)由点C在以O为圆心5为半径的上半圆上运动,推出以C为圆心2为半径的圆刚好与弧HK相切,此时要想弧HK上任意两点都是圆C的平衡点,需要满足CK≤6,CH≤6,分两种情形分别求出b的值即可判断.
解:(1)①由题意知:OA=3,OB=![]() ,则d的最小值是3,最大值是
,则d的最小值是3,最大值是![]() ;
;
②根据平衡点的定义,点P1与点O是线段AB的一对平衡点,
故答案为3,![]() ,P1;
,P1;
(2)如图2中,
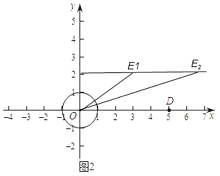
由题意点D到⊙O的最近距离是4,最远距离是6,
∵点D与点E是⊙O的一对平衡点,此时需要满足E1到⊙O的最大距离是4,即OE1=3,可得x=![]() ,
,
同理:当E2到⊙的最小距离为是6时,OE2=7,此时x=![]() ,
,
综上所述,满足条件的x的值为![]() ≤x≤
≤x≤![]() ;
;
(3)∵点C在以O为圆心5为半径的上半圆上运动,
∴以C为圆心2为半径的圆刚好与弧HK 相切,此时要想弧HK上任意两点都是圆C的平衡点需要满足CK≤6,CH≤6,如图3-1中,当CK=6时,作CM⊥HK于M.
则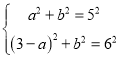 ,解得:
,解得: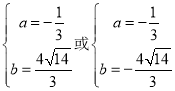 (舍去),
(舍去),
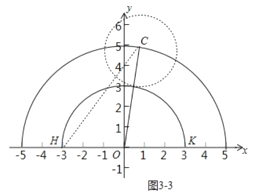
如图3-3中,当CH=6时,同法可得a=![]() ,b=
,b=![]() ,
,
在两者中间时,a=0,b=5,观察图象可知:满足条件的b的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】改革开放40年以来,城乡居民生活水平持续快速提升.居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出.下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图:
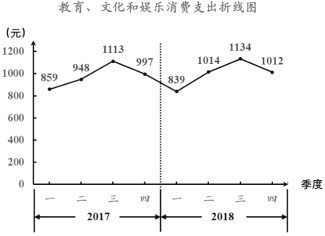
说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.
根据上述信息,下列结论中错误的是( ).
A.2017年第二季度环比有所提高B.2017年第四季度环比有所下降
C.2018年第一季度同比有所提高D.2017和2018年支出最高的都是第三季度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的网格是正方形网格,则
 __________
__________ (点
(点 ,
, ,
, ,
, ,
, 是网格线交点).
是网格线交点).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数
50
100
150
200
250
300
350
400
450
500
“正面向上”次数
22
52
68
101
116
147
160
187
214
238
“正面向上”频率
0.44
0.52
0.45
0.51
0.46
0.49
0.46
0.47
0.48
0.48
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=a
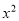 -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-
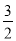 a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是
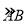 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.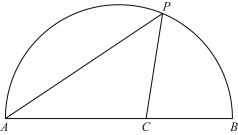
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是
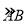 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:AP/cm
0
1.00
2.00
3.00
4.00
5.00
6.00
PC/cm
0
1.21
2.09
2.69
m
2.82
0
AC/cm
0
0.87
1.57
2.20
2.83
3.61
6.00
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定
 的长度是自变量,
的长度是自变量, 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
相关试题

