【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
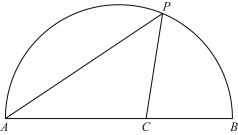
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
参考答案:
【答案】(1)①3.0;②AP的长度是自变量,PC的长度和AC的长度都是这个自变量的函数;(答案不唯一);(2)见解析; (3)2.3或4.2
【解析】
(1)①根据题意AC的值分析得出PC的值接近于半径;
②由题意AP的长度是自变量,分析函数值即可;
(2)利用描点法画出函数图像即可;
(3)利用数形结合的思想解决问题即可.
解:(1)①AC=2.83可知PC接近于半径3.0;
②AP的长度是自变量,PC的长度和AC的长度都是这个自变量的函数;(答案不唯一)
(2)如图(答案不唯一,和(1)问相对应);
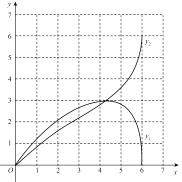

(3)结合图像根据AP=PC以及AC=PC进行代入分析可得AP为2.3或4.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,对于两个点
中,对于两个点 ,
, 和图形
和图形 ,如果在图形
,如果在图形 上存在点
上存在点 ,
, (
( ,
, 可以重合)使得
可以重合)使得 ,那么称点
,那么称点 与点
与点 是图形
是图形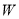 的一对平衡点.
的一对平衡点.(1)如图1,已知点
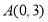 ,
,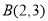 ;
;①设点
 与线段
与线段 上一点的距离为
上一点的距离为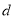 ,则
,则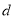 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;②在
 ,
, ,
,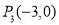 这三个点中,与点
这三个点中,与点 是线段
是线段 的一对平衡点的是 ;
的一对平衡点的是 ;(2)如图2,已知
 的半径为1,点
的半径为1,点 的坐标为
的坐标为.若点 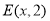 在第一象限,且点
在第一象限,且点 与点
与点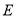 是
是 的一对平衡点,求
的一对平衡点,求 的取值范围;
的取值范围;(3)如图3,已知点
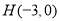 ,以点
,以点 为圆心,
为圆心, 长为半径画弧交
长为半径画弧交 的正半轴于点
的正半轴于点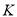 .点
.点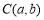 (其中
(其中 )是坐标平面内一个动点,且
)是坐标平面内一个动点,且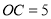 ,
,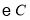 是以点
是以点 为圆心,半径为2的圆,若
为圆心,半径为2的圆,若 上的任意两个点都是
上的任意两个点都是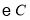 的一对平衡点,直接写出
的一对平衡点,直接写出 的取值范围.
的取值范围.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=a
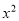 -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-
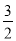 a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若
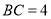 ,
,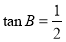 ,求OB.
,求OB. -
科目: 来源: 题型:
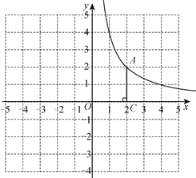
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,函数
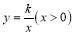 的图象经过点
的图象经过点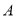 ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.(1)求k的值;
(2)直线AB:
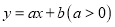 图象经过点
图象经过点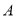 交x轴于点
交x轴于点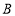 .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.①直线AB经过
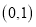 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学竞赛中有5道选择题,每题1分,每道题在
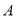 、
、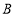 、
、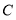 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:第一题
第二题
第三题
第四题
第五题
得分
甲
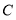
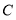
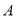
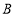
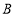
4
乙
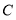
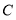
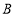
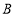
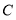
3
丙
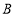
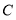
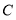
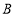
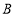
2
丁
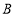
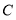
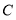
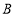
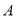
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
相关试题

