【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E. 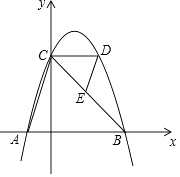
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比.
参考答案:
【答案】
(1)解:∵令y=0,则﹣(x﹣1)2+4=0,解得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0)
(2)解:∵CD∥AB,DE∥AC,
∴△CDE∽△BAC.
∵当y=3时,x1=0,x2=2,
∴CD=2.
∵AB=4,
∴ ![]() =
= ![]() ,
,
∴ ![]() =(
=( ![]() )2=
)2= ![]()
【解析】(1)直接把y=0代入求出x的值即可;(2)先根据CD∥AB,DE∥AC得出△CDE∽△BAC,求出CD的长,再由相似三角形的性质即可得出结论.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】讲完“有理数的除法”后,老师在课堂上出了一道计算题:15
 ÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.
÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.方法一:原式=
 ×(-
×(- )=-
)=- =-1
=-1 ;
;方法二:原式=(15+
 )×(-
)×(- )=15×(-
)=15×(- )+
)+ ×(-
×(- )=-
)=- =-1
=-1 ;
;方法三:原式=(16-
 )÷(-8)=16÷(-8)-
)÷(-8)=16÷(-8)- ÷(-8)=-2+
÷(-8)=-2+ =-1
=-1 .
.对这三种方法,大家议论纷纷,你认为哪种方法最好?请说出理由,并说说本题对你有何启发.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
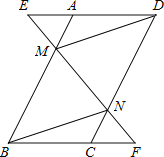
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽有5张写着不同数的卡片,请你按要求抽出卡片,完成下列各题:

(1)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相乘再相除的结果最大?最大值是多少?
(2)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相除再相乘的结果最小?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
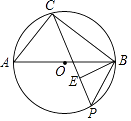
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
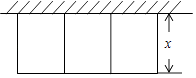
(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.
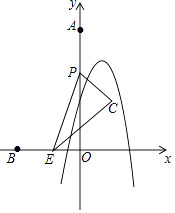
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值.
相关试题

