【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
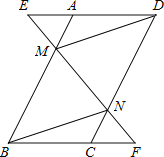
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM![]() DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
DN,则由有一组对边平行且相等的四边形是平行四边形即可证明.
证明:(1)四边形ABCD是平行四边形,
∴∠DAB=∠BCD,
∴∠EAM=∠FCN,
又∵AD∥BC,
∴∠E=∠F.
∵在△AEM与△CFN中,
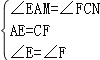 ,
,
∴△AEM≌△CFN(ASA);
(2)∵四边形ABCD是平行四边形,
∴AB![]() CD,
CD,
又由(1)得AM=CN,
∴BM![]() DN,
DN,
∴四边形BMDN是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD.
如图1,你能得出∠A+∠E+∠C=360°吗?
如图2,猜想出∠A.∠C、∠E的关系式并说明理由.
如图3,∠A.∠C、∠E的关系式又是什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A.
 B. 3 C. 1 D.
B. 3 C. 1 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】讲完“有理数的除法”后,老师在课堂上出了一道计算题:15
 ÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.
÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.方法一:原式=
 ×(-
×(- )=-
)=- =-1
=-1 ;
;方法二:原式=(15+
 )×(-
)×(- )=15×(-
)=15×(- )+
)+ ×(-
×(- )=-
)=- =-1
=-1 ;
;方法三:原式=(16-
 )÷(-8)=16÷(-8)-
)÷(-8)=16÷(-8)- ÷(-8)=-2+
÷(-8)=-2+ =-1
=-1 .
.对这三种方法,大家议论纷纷,你认为哪种方法最好?请说出理由,并说说本题对你有何启发.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽有5张写着不同数的卡片,请你按要求抽出卡片,完成下列各题:

(1)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相乘再相除的结果最大?最大值是多少?
(2)从中取出3张卡片,如何抽取才能使这3张卡片上的数依次先相除再相乘的结果最小?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣(x﹣1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E.
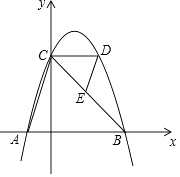
(1)求A,B两点的坐标;
(2)求△CDE与△BAC的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
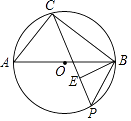
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.
相关试题

