【题目】如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( ) 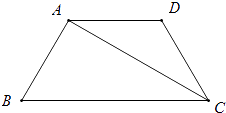
A.12 ![]()
B.15 ![]()
C.12
D.15
参考答案:
【答案】D
【解析】解:过点A作AE∥CD,交BC于点E, ∵梯形ABCD是等腰梯形,∠B=60°,
∴AD∥BC,
∴四边形ADCE是平行四边形,
∴∠AEB=∠BCD=60°,
∵CA平分∠BCD,
∴∠ACE= ![]() ∠BCD=30°,
∠BCD=30°,
∵∠AEB是△ACE的外角,
∴∠AEB=∠ACE+∠EAC,即60°=30°+∠EAC,
∴∠EAC=30°,
∴AE=CE=3,
∴四边形ADEC是菱形,
∵△ABE中,∠B=∠AEB=60°,
∴△ABE是等边三角形,
∴AB=BE=AE=3,
∴梯形ABCD的周长=AB+(BE+CE)+CD+AD=3+3+3+3+3=15.
故选:D.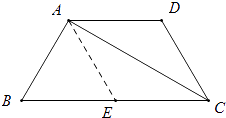
【考点精析】解答此题的关键在于理解等腰梯形的性质的相关知识,掌握等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
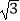 ,CE=1.则
,CE=1.则 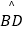 的长是( )
的长是( ) 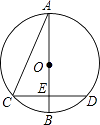
A.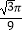
B.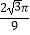
C.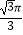
D.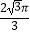
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,A(-1,0),B(1,0),C(0,1),点D为x轴正半轴上的一个动点,点E为第一象限内一点,且CE⊥CD,CE=CD.
(1)试说明:∠EBC=∠CAB ;
(2)取DE的中点F,连接OF,试判断OF与AC的位置关系,并说明理由;
(3)在(2)的条件下,试探索O、D、F三点能否构成等腰三角形,若能,请直接写出所有符合条件的点D的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+
 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是  ,矩形的周长是2(x+
,矩形的周长是2(x+  );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=  (x>0),解得x=1,这时矩形的周长2(x+
(x>0),解得x=1,这时矩形的周长2(x+  )=4最小,因此x+
)=4最小,因此x+  (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子  (x>0)的最小值是( )
(x>0)的最小值是( )
A.2
B.1
C.6
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个等式.例
如图1可以得到
 .请解答下列问题:
.请解答下列问题:
(1)根据图2,完成数学等式:
 = ;
= ;(2)观察图3,写出图3中所表示的等式: =____________.
(3)若
 、
、 、
、 ,且
,且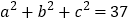 ,请利用(2)所得的结论求:
,请利用(2)所得的结论求: 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
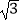 ,CE=1.则
,CE=1.则  的长是( )
的长是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+
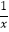 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 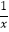 ,矩形的周长是2(x+
,矩形的周长是2(x+ 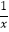 );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x= 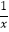 (x>0),解得x=1,这时矩形的周长2(x+
(x>0),解得x=1,这时矩形的周长2(x+ 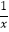 )=4最小,因此x+
)=4最小,因此x+ 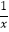 (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子 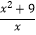 (x>0)的最小值是( )
(x>0)的最小值是( )
A.2
B.1
C.6
D.10
相关试题

