【题目】张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子x+ ![]() (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ![]() ,矩形的周长是2(x+
,矩形的周长是2(x+ ![]() );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x= ![]() (x>0),解得x=1,这时矩形的周长2(x+
(x>0),解得x=1,这时矩形的周长2(x+ ![]() )=4最小,因此x+
)=4最小,因此x+ ![]() (x>0)的最小值是2.模仿张华的推导,你求得式子
(x>0)的最小值是2.模仿张华的推导,你求得式子 ![]() (x>0)的最小值是( )
(x>0)的最小值是( )
A.2
B.1
C.6
D.10
参考答案:
【答案】C
【解析】解:∵x>0, ∴在原式中分母分子同除以x,
即 ![]() =x+
=x+ ![]() ,
,
在面积是9的矩形中设矩形的一边长为x,则另一边长是 ![]() ,
,
矩形的周长是2(x+ ![]() );
);
当矩形成为正方形时,就有x= ![]() ,(x>0),
,(x>0),
解得x=3,
这时矩形的周长2(x+ ![]() )=12最小,
)=12最小,
因此x+ ![]() (x>0)的最小值是6.
(x>0)的最小值是6.
故选:C
【考点精析】利用分式的混合运算和完全平方公式对题目进行判断即可得到答案,需要熟知运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方.
-
科目: 来源: 题型:
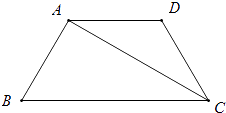
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( )
A.12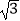
B.15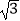
C.12
D.15 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个等式.例
如图1可以得到
 .请解答下列问题:
.请解答下列问题:
(1)根据图2,完成数学等式:
 = ;
= ;(2)观察图3,写出图3中所表示的等式: =____________.
(3)若
 、
、 、
、 ,且
,且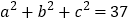 ,请利用(2)所得的结论求:
,请利用(2)所得的结论求: 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=
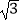 ,CE=1.则
,CE=1.则  的长是( )
的长是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列文字与例题,并解答:
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法.
例如:以下式子的分解因式的方法就称为分组分解法.
A2+2ab+b2+ac+bc
原式=(a2+2ab+b2)+ac+bc
=(a+b)2+c(a+b)
=(a+b)(a+b+c)
(1)试用“分组分解法”因式分解:

(2)已知四个实数a,b,c,d,满足a≠b,c≠d,并且aa+ac=12k,b2+bc=12k,c2+ac=24k,d2+ad=24k
,同时成立.
①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示
 、
、 、
、 (直接写出答案即可).
(直接写出答案即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1,
 ,3 B.
,3 B.  ,
, 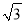 ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D.  ,
,  ,
, 
【答案】C
【解析】A、12+(
 )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;B、(
 2+(
2+( )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(
 ))2+(
))2+( )2≠(
)2≠( )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.故选:C.
【题型】单选题
【结束】
3【题目】在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A)
 (B)
(B) (C)9 (D)6
(C)9 (D)6 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算:( ﹣2)0+(﹣1)2014+
﹣2)0+(﹣1)2014+ 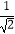 ﹣sin45°;
﹣sin45°;
(2)先化简,再求值:(a2b+ab)÷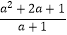 ,其中a=
,其中a=  +1,b=
+1,b=  ﹣1.
﹣1.
相关试题

