【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 . 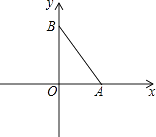
参考答案:
【答案】(3,4)或( ![]() ,
,![]() )或(﹣
)或(﹣ ![]() ,
,![]() )
)
【解析】解:如图所示:①∵OA=3,OB=4,
∴P1(3,4);②连结OP2,
设AB的解析式为y=kx+b,则
![]() ,
,
解得  .
.
故AB的解析式为y=﹣ ![]() x+4,
x+4,
则OP2的解析式为y= ![]() x,
x,
联立方程组得  ,
,
解得  ,
,
则P2( ![]() ,
, ![]() );③连结P2P3,
);③连结P2P3,
∵(3+0)÷2=1.5,
(0+4)÷2=2,
∴E(1.5,2),
∵1.5×2﹣ ![]() =﹣
=﹣ ![]() ,
,
2×2﹣ ![]() =
= ![]() ,
,
∴P3(﹣ ![]() ,
, ![]() ).
).
故点P的坐标为(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
所以答案是:(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对雾霾天气的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
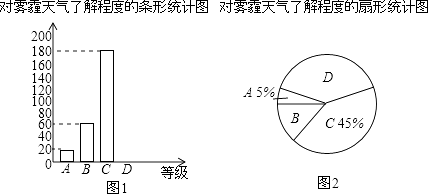
对雾霾的了解程度
百分比
A.非常了解
5%
A.比较了解
15%
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有人,n=;扇形统计图中D部分扇形所对应的圆心角是度;
(2)请补全条形统计图;
(3)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照下列要求画图并填空:
如图,点
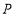 是
是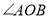 的边
的边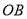 上的一点,
上的一点,(1)过点
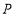 作
作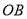 的垂线,交
的垂线,交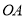 于点
于点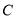 ;
;(2)在(1)的基础上作
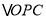 的边
的边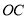 上的高,垂足为
上的高,垂足为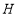 ;
;(3)线段___________的长度是点
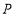 到直线
到直线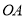 的距离;
的距离;(4)线段
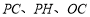 这三条线段大小关系是___________(用“<”号连接).
这三条线段大小关系是___________(用“<”号连接).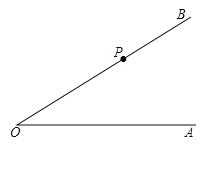
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足下列条件的△ABC不是直角三角形的是()
A. BC=1,AC=2,AB=

B. BC=1,AC=2,AB=
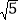
C. BC:AC:AB=3:4:5
D. ∠A:∠B:∠C=3:4:5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在校园文化建设中,某学校原计划按每班5幅订购了“名人字画”共90幅.由于新学期班数增加,决定从阅览室中取若干幅“名人字画”一起分发,如果每班分4幅,则剩下17幅;如果每班分5幅,则最后一班不足3幅,但不少于1幅.
(1)该校原有的班数是多少个?
(2)新学期所增加的班数是多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以
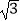 cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts. 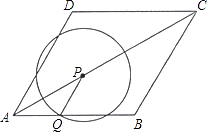
(1)当P异于A、C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b的图象交反比例函数
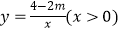 图象于点A,B,交x轴于点C.
图象于点A,B,交x轴于点C.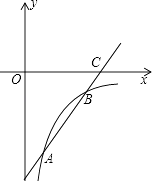
(1)求m的取值范围;
(2)若点A的坐标是(1,﹣4),且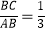 ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;
(3)在(2)的情况下,请直接写出不等式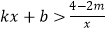 的解集.
的解集.
相关试题

