【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E. 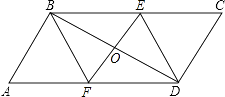
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形,O是BD中点,
∴BC∥AD,OB=OD,
∴∠OBE=∠ODF,
又∵∠BOE=∠DOF,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形
(2)解:当四边形BEDF是菱形时,根据菱形的性质可得:EF与BD互相垂直平分
(3)解:∵四边形BEDF是矩形
∴∠AFB=90°
又∵∠A=60°,
∴∠ABF=30°,
∴AF= ![]() AB=
AB= ![]() ×4=2,
×4=2,
∴Rt△ABF中,BF=2 ![]() ,
,
又∵AD=BC=6,
∴DF=6﹣2=4,
∴矩形BEDF的面积=BF×DF=2 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;(2)根据根据菱形的性质作出判断:EF与BD互相垂直平分;(3)根据Rt△ABF的边角关系,求得BF和AF,再根据矩形的性质,求得DF的长,最后计算矩形的面积.
【考点精析】掌握平行四边形的判定与性质和矩形的性质是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°.
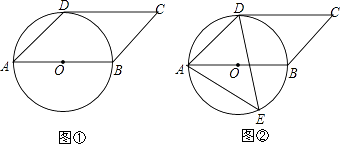
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AC 是对角线,AB=CD,∠DAC+∠BCA=180°,∠BAC+∠ACD=90°,四边形 ABCD 的面积是 18,则 CD 的长是__________.
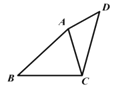
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生每天零花钱情况,对我校初二学年某班 50 名同学每天零花钱情况进行 了统计,并绘制成下面的统计图.
(1)直接写出这 50 名同学零花钱数据的众数是_____;中位数是________.
(2)求这 50 名同学零花钱的平均数.
(3)该校共有学生 3100 人,请你根据该班的零花钱情况,估计这个中学学生每天的零花 钱不小于 30 元的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是 ( ).

A. 9cm≤h≤10cm B. 10cm≤h≤11cm C. 12cm≤h≤13cm D. 8cm≤h≤9cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,购进 4 件甲种商品比购进 5 件乙种商品少用 10 元,购 进 20 件甲种商品和 10 件乙种商品共用去 160 元.
(1)求甲、乙两种商品每件进价分别是多少元?
(2)若该商店购进甲、乙两种商品共 140 件,都标价 10 元出售,售出一部分降价促销, 以标价的八折售完所有剩余商品,以 10 元售出的商品件数比购进甲种商品件数少 20 件,该商店此次购进甲、乙两种商品降价前后共获利不少于 420 元,求至少购进甲种商品多少件?
相关试题

