【题目】已知四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,∠DAB=45°. 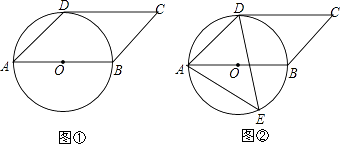
(1)如图①,判断CD与⊙O的位置关系,并说明理由;
(2)如图②,E是⊙O上一点,且点E在AB的下方,若⊙O的半径为3cm,AE=5cm,求点E到AB的距离.
参考答案:
【答案】
(1)解:(1)CD与圆O相切.
证明:如图①,连接OD,
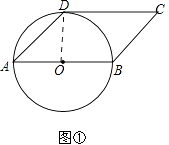
则∠AOD=2∠DAB=2×45°=90°,
∵四边形ABCD是平行四边形,
∴AB∥DC.
∴∠CDO=∠AOD=90°.
∴OD⊥CD.
∴CD与圆O相切.
(2)如图②,作EF⊥AB于F,连接BE,
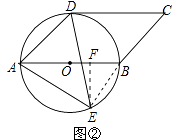
∵AB是圆O的直径,
∴∠AEB=90°,AB=2×3=6.
∵AE=5,
∴BE= ![]() =
= ![]() ,
,
∵sin∠BAE= ![]() .
.
∴ ![]() =
= ![]()
∴EF= ![]() .
.
【解析】(1)连接OD,则∠AOD为直角,由四边形ABCD是平行四边形,则AB∥DC.从而得出∠CDO=90°,即可证出答案.(2)作EF⊥AB于F,连接BE,根据圆周角定理得∠AEB=90°,然后根据勾股定理求得BE,然后根据sin∠BAE= ![]() 求得EF即可.
求得EF即可.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天,李玉刚同学随爸爸妈妈会老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km/h.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,AC 是对角线,AB=CD,∠DAC+∠BCA=180°,∠BAC+∠ACD=90°,四边形 ABCD 的面积是 18,则 CD 的长是__________.
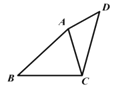
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生每天零花钱情况,对我校初二学年某班 50 名同学每天零花钱情况进行 了统计,并绘制成下面的统计图.
(1)直接写出这 50 名同学零花钱数据的众数是_____;中位数是________.
(2)求这 50 名同学零花钱的平均数.
(3)该校共有学生 3100 人,请你根据该班的零花钱情况,估计这个中学学生每天的零花 钱不小于 30 元的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E.
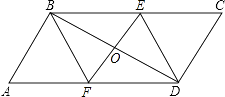
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
相关试题

