【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式. 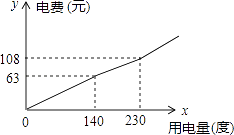
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
参考答案:
【答案】
(1)140<x≤230;x>230
(2)54
(3)解:设第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y=ax+c,
将(140,63),(230,108)代入得出:
![]() ,
,
解得: 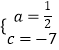 ,
,
则第二档每月电费y(元)与用电量x(度)之间的函数关系式为:y= ![]() x﹣7(140<x≤230)
x﹣7(140<x≤230)
(4)解:根据图象可得出:用电230度,需要付费108元,用电140度,需要付费63元,
故,108﹣63=45(元),230﹣140=90(度),
45÷90=0.5(元/度),
则第二档电费为0.5元/度;
∵小刚家某月用电290度,交电费153元,
290﹣230=60(度),153﹣108=45(元),
45÷60=0.75(元/度),
m=0.75﹣0.5=0.25,
答:m的值为0.25
【解析】解:(1)利用函数图象可以得出,阶梯电价方案分为三个档次,利用横坐标可得出: 第二档:140<x≤230,第三档x>230;
2)根据第一档范围是:0<x≤140,
根据图象上点的坐标得出:设解析式为:y=kx,将(140,63)代入得出:k= ![]() =0.45,
=0.45,
故y=0.45x,
当x=120,y=0.45×120=54(元),
所以答案是:54;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA.

(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形的周长为24,相邻两内角比为1:2,则其对角线长分别为____________
-
科目: 来源: 题型:
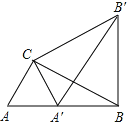
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,则BB′的长度为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=
 ,那么AC的长等于__________ .
,那么AC的长等于__________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,这是一种数值转换机的运算程序.
(1)若第1次输入的数为2,则第1次输出的数为1,那么第2次输出的数为4;若第1次输入的数为12,则第5次输出的数为__________.
(2)若输入的数为5,求第2016次输出的数是多少.
(3)是否存在输入的数x,使第3次输出的数是x?若存在,求出所有x的值;若不存在,请说明理由.

相关试题

