【题目】已知:如图,这是一种数值转换机的运算程序.
(1)若第1次输入的数为2,则第1次输出的数为1,那么第2次输出的数为4;若第1次输入的数为12,则第5次输出的数为__________.
(2)若输入的数为5,求第2016次输出的数是多少.
(3)是否存在输入的数x,使第3次输出的数是x?若存在,求出所有x的值;若不存在,请说明理由.

参考答案:
【答案】(1)4、6.(2)2;(3)0,1,2,4.
【解析】
试题(1)根据数值转换机的运算程序,以及有理数的混合运算的运算方法,求出第1次输入的数为2时,第2次输出的数为多少,以及第1次输入的数为12时,第5次输出的数为多少即可.
(2)根据数值转换机的运算程序,以及有理数的混合运算的运算方法,求出若输入的数为5,每次输出的数的规律,判断出第2016次输出的数是多少即可.
(3)分x为奇数,x为偶数两种情况,根据输入的数x,使第3次输出的数是x,路程方程求解即可.
试题解析:(1)∵1+3=4,
∴第1次输出的数为1,则第2次输出的数为4.
![]() ×12=6,6×
×12=6,6×![]() =3,3+3=6,6×
=3,3+3=6,6×![]() =3,3+3=6,
=3,3+3=6,
∴第1次输入的数为12,则第5次输出的数为6.
(2)5+3=8,8×![]() =4,4×
=4,4×![]() =2,2×
=2,2×![]() =1,1+3=4,
=1,1+3=4,
∴若输入的数为5,则每次输出的数分别是8、4、2、1、4、2、1,…,
(20161)÷3=2015÷3=671…2
∴第2016次输出的数是2.
(3)当x为奇数时,有![]() (x+3)+3=x,解得x=9(舍去),
(x+3)+3=x,解得x=9(舍去),
![]() ×
×![]() (x+3)=x,解得x=1,
(x+3)=x,解得x=1,
当x为偶数时,有![]() ×
×![]() ×
×![]() x=x,解得x=0,
x=x,解得x=0,
![]() ×
×![]() x+3=x,解得x=4,
x+3=x,解得x=4,
![]() ×(
×(![]() x+3)=x,解得x=2,
x+3)=x,解得x=2,
综上所述,x=0或1或2或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
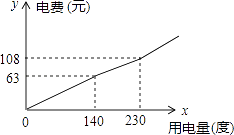
(1)根据图象,阶梯电价方案分为三个档次,填写下表:档次
第一档
第二档
第三档
每月用电量x(度)
0<x≤140
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=
 ,那么AC的长等于__________ .
,那么AC的长等于__________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某牛奶厂在一条南北走向的大街上设有O,A,B,C四家特约经销店.A店位于O店的南面3千米处;B店位于O店的北面1千米处,C店在O店的北面2千米处.
(1)请以O为原点,向北的方向为正方向,1个单位长度表示1千米,画一条数轴,你能在数轴上分别表示出O,A,B,C的位置吗?
(2)牛奶厂的送货车从O店出发,要把一车牛奶分别送到A,B,C三家经销店,那么送货车走的最短路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解初二年级480名学生到校上学的方式,在初二随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).


⑴问:在这次调查中,一共抽取了多少名学生?
⑵补全条形统计图;
⑶估计该校初二年级学生中有多少人乘坐公交车上学.
相关试题

