【题目】如图,△OAC中,以O为圆心,OA为半径作⊙O,作OB⊥OC交⊙O于B,垂足为O,连接AB交OC于点D,∠CAD=∠CDA. 
(1)判断AC与⊙O的位置关系,并证明你的结论;
(2)若OA=5,OD=1,求线段AC的长.
参考答案:
【答案】
(1)解:线段AC是⊙O的切线;
理由如下:∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换);
又∵OA=OB(⊙O的半径),
∴∠B=∠OAB(等边对等角);
∵OB⊥OC(已知),
∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,
∴线段AC是⊙O的切线

(2)解:设AC=x(x>0).
∵∠CAD=∠CDA(已知),
∴DC=AC=x(等角对等边);
∵OA=5,OD=1,
∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,
OC2=AC2+OA2,即
(1+x)2=x2+52,
解得x=12,即AC=12.
【解析】(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°.所以线段AC是⊙O的切线;(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在Rt△OAC中,根据勾股定理来求AC的长度.
【考点精析】关于本题考查的勾股定理的概念和切线的判定定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据遵义市统计局发布的2011年遵义市国民经济和社会发展统计公报相关数据,我市2011年社会消费品总额按城乡划分绘制统计图①,2010年与2011年社会消费品销售额按行业划分绘制条形统计图②,根据图中信息回答下列问题:
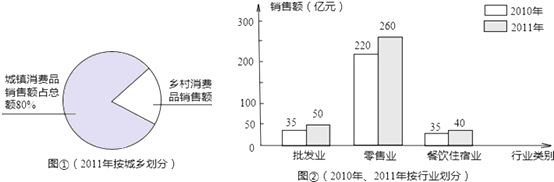
(1)图①中“乡村消费品销售额”的圆心角是度,乡村消费品销售额为亿元;
(2)2010年到2011年间,批发业、零售业、餐饮住宿业中销售额增长的百分数最大的行业是;
(3)预计2013年我市的社会消品总销售额到达504亿元,求我市2011﹣2013年社会消费品销售总额的年平均增长率. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】将7张如图1所示的长为a,宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,求a,b满足的条件.
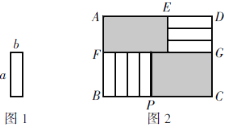
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形的周长为24,相邻两内角比为1:2,则其对角线长分别为____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,则BB′的长度为
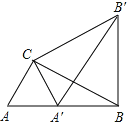
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
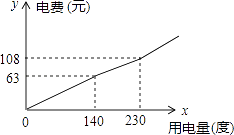
(1)根据图象,阶梯电价方案分为三个档次,填写下表:档次
第一档
第二档
第三档
每月用电量x(度)
0<x≤140
(2)小明家某月用电120度,需交电费元;
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.
相关试题

