【题目】(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.

(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.

(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;

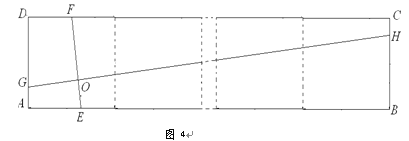
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
参考答案:
【答案】(1) 证明:如图1,

∵ 四边形ABCD为正方形,
∴ AB=BC,∠ABC=∠BCD=90°,
∴ ∠EAB+∠AEB=90°.
∵ ∠EOB=∠AOF=90°,
∴ ∠FBC+∠AEB=90°,∴ ∠EAB=∠FBC,
∴ △ABE≌△BCF , ∴ BE=CF. ………………3分
(2) 解:如图2,过点A作AM//GH交BC于M,
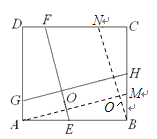
过点B作BN//EF交CD于N,AM与BN交于点O/,
则四边形AMHG和四边形BNFE均为平行四边形,
∴ EF=BN,GH=AM,
∵ ∠FOH=90°, AM//GH,EF//BN, ∴ ∠NO/A=90°,
故由(1)得, △ABM≌△BCN, ∴ AM=BN,
∴ GH=EF=4. ………………6分
(3) ① 8.② 4n. ………………8分
【解析】(1)关键是证出∠CBF=∠BAE,可利用同角的余角相等得出,从而结合已知条件,利用SAS可证△ABE≌△BCF,于是BE=CF;
(2)过A作AM∥GH,交BC于M,过B作BN∥EF,交CD于N,AMBN交于点O′,利用平行四边形的判定,可知四边形AMHG和四边形BNFE是,那么AM=GH,BN=EF,由于∠EOH=90°,结合平行线的性质,可知∠AO′N=90°,那么此题就转化成(1),求△BCN≌△ABM即可;
(3)①若是两个正方形,则GH=2EF=8;②若是n个正方形,那么GH=n4=4n.
-
科目: 来源: 题型:
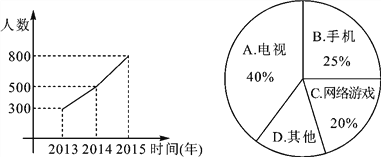
查看答案和解析>>【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了了解学生的视力变化情况,从全市九年级随机抽取了1 500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
解答下列问题:
(1)图中D所在扇形的圆心角度数为______;
(2)若2016年全市共有30 000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB切⊙O于点B,连结OA交⊙O于点C,连结OB.若∠A=30°,OA=4,则劣弧
 的长是( )
的长是( ) 
A. π
π
B. π
π
C.π
D. π
π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC和等腰Rt△DEF均内接于⊙O,∠D=Rt∠,EF∥AC,AC分别交DE,DF于点P,Q,EF分别交AB,BC于点G,H,则
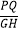 的值是( )
的值是( ) 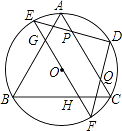
A.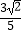
B.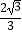
C.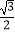
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,某市政府的一项实事工程就是由政府投入1 000万元资金,对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造,某社区为配合政府完成该项工作,对社区内1 200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况
均不改造
改造水龙头
改造马桶
1个
2个
3个
4个
1个
2个
户数
20
31
28
21
12
69
2
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户;
(2)改造后,一个水龙头一年大概可节约5吨水,一个马桶一年大约可节约15吨水,试估计该社区一年共可节约多少吨水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次模拟考试后,数学陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的百分比之和是14%;②第一组的百分比是2%;③自左到右第二、三、四组的频数比为3∶9∶8,然后布置学生(也请你一起)结合统计图完成下列问题:
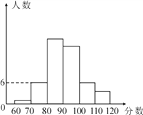
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x
人数
60≤x<80
2
80≤x<100
5
100≤x<120
21
120≤x<140
13
140≤x<160
8
160≤x<180
4
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
相关试题

