搜索
【题目】如图，AB切⊙O于点B，连结OA交⊙O于点C，连结OB．若∠A=30°，OA=4，则劣弧 
的长是（ ） 
A.
π
B.
π
C.π
D.
π
参考答案：
【答案】B
【解析】解：∵AB切⊙O于点B，
∴∠ABO=90°，
∵∠A=30°，
∴∠O=60°，
∵OA=4，
∴OB= 
OA=2，
∴劣弧 
的长= 
= 
π，
故选B．
【考点精析】认真审题，首先需要了解切线的性质定理(切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)，还要掌握弧长计算公式(若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的)的相关知识才是答题的关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】仔细阅读下面例题，解答问题
例题：已知二次三项式x2﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．
解：设另一个因式为（x+n），得x2﹣4x+m＝（x+3）（x+n），
则x2﹣4x+m＝x2+（n+3）x+3n
∴
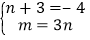
解得：n＝﹣7，m＝﹣21．
∴另一个因式为（x﹣7），m的值为﹣21．
问题：
（1）若二次三项式x2﹣5x+6可分解为（x﹣2）（x+a），则a＝ ；
（2）若二次三项式2x2+bx﹣5可分解为（2x﹣1）（x+5），则b＝ ；
（3）仿照以上方法解答下面问题：若二次三项式2x2+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校测量了九年级(1)班学生的身高(精确到1cm)，按10cm为一段进行分组，得到如下频数分布直方图如图，则下列说法不正确的是( )
A. 该班人数最多的身高段的学生数为20人
B. 该班身高低于160.5 cm的学生数为20人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
-
科目： 来源： 题型：
查看答案和解析>>【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等，视力日渐减退，某市为了了解学生的视力变化情况，从全市九年级随机抽取了1 500名学生，统计了每个人连续三年视力检查的结果，根据视力在4.9以下的人数变化制成折线统计图，并对视力下降的主要因素进行调查，制成扇形统计图．
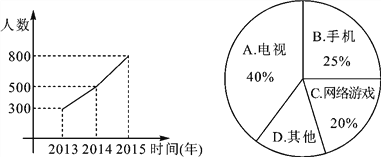
解答下列问题：
(1)图中D所在扇形的圆心角度数为______；
(2)若2016年全市共有30 000名九年级学生，请你估计视力在4.9以下的学生约有多少名？
(3)根据扇形统计图信息，你觉得中学生应该如何保护视力？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边△ABC和等腰Rt△DEF均内接于⊙O，∠D=Rt∠，EF∥AC，AC分别交DE，DF于点P，Q，EF分别交AB，BC于点G，H，则
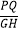的值是（ ）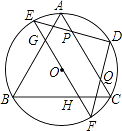 
A.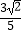
B.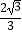
C.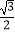
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF＝90°.求证：BE＝CF.
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH＝90°, EF＝4.求GH的长.
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,∠FOH＝90°,EF＝4. 直接写出下列两题的答案：
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
-
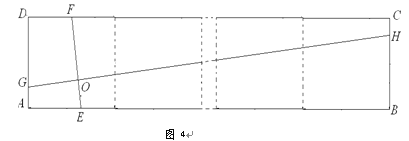
科目： 来源： 题型：
查看答案和解析>>【题目】今年，某市政府的一项实事工程就是由政府投入1 000万元资金，对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造，某社区为配合政府完成该项工作，对社区内1 200户家庭中的120户进行了随机抽样调查，并汇总成下表：
改造情况
均不改造
改造水龙头
改造马桶
1个
2个
3个
4个
1个
2个
户数
20
31
28
21
12
69
2
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户；
(2)改造后，一个水龙头一年大概可节约5吨水，一个马桶一年大约可节约15吨水，试估计该社区一年共可节约多少吨水？
(3)在抽样的120户家庭中，既要改造水龙头又要改造马桶的家庭共有多少户？
相关试题
