【题目】如图,在△ABC中,tanA=![]() ,∠B=45°,AB=14. 求BC的长.
,∠B=45°,AB=14. 求BC的长.

参考答案:
【答案】∴BC=6![]()
【解析】试题分析:
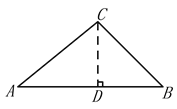
如图,过点C作CD⊥AB于点D,得到Rt△ADC和Rt△BCD,由在Rt△ADC中tanA=![]() ,设CD=3x,AD=4x,则在Rt△BCD中,由∠B=45°,可得BD=CD=3x,结合AB=14由勾股定理列出方程解得x的值,再在Rt△BCD中,由勾股定理即可求得BC的值.
,设CD=3x,AD=4x,则在Rt△BCD中,由∠B=45°,可得BD=CD=3x,结合AB=14由勾股定理列出方程解得x的值,再在Rt△BCD中,由勾股定理即可求得BC的值.
试题解析:
如图,过点C作CD⊥AB于点D,
∴∠ADC=∠BDC=90°,
∵tanA=![]() ,
,
∴![]() ,
,
设CD=3x,则AD=4x,
∵∠B=45°,∠BDC=90°,
∴BD=CD=3x,
∵AD+BD=AB=14,
∴4x+3x=14,解得x=2,
∴BD=CD=6,
∴BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),交y轴于点A(0,a),且a、p满足
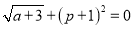 .
.(1)求直线AP的解析式;
(2)如图1,点P关于y轴的对称点为Q,R(0,2),点S在直线AQ上,且SR=SA,求直线RS的解析式和点S的坐标;
(3)如图2,点B(﹣2,b)为直线AP上一点,以AB为斜边作等腰直角三角形ABC,点C在第一象限,D为线段OP上一动点,连接DC,以DC为直角边,点D为直角顶点作等腰三角形DCE,EF⊥x轴,F为垂足,下列结论:①2DP+EF的值不变;②
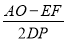 的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.
的值不变;其中只有一个结论正确,请你选择出正确的结论,并求出其定值.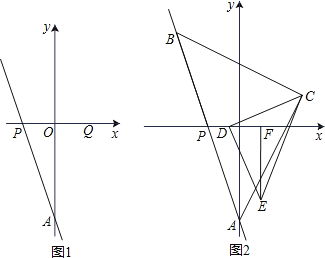
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式的规律,解答下列问题:
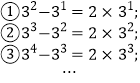
(1)按此规律,第④个等式为_________;第
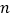 个等式为_______;(用含
个等式为_______;(用含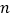 的代数式表示,
的代数式表示,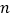 为正整数)
为正整数)(2)按此规律,计算:
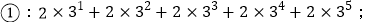
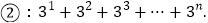
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点
 表示的数是
表示的数是 点
点 在点
在点 的右侧,且到点
的右侧,且到点 的距离是18;点
的距离是18;点 在点
在点 与点
与点 之间,且到点
之间,且到点 的距离是到点
的距离是到点 距离的2倍.
距离的2倍.(1)点
 表示的数是____________;点
表示的数是____________;点 表示的数是_________;
表示的数是_________;(2)若点P从点
 出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为
出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为 秒,在运动过程中,当
秒,在运动过程中,当 为何值时,点P与点Q之间的距离为6?
为何值时,点P与点Q之间的距离为6?(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为
 在运动过程中,是否存在某一时刻使得
在运动过程中,是否存在某一时刻使得 ?若存在,请求出此时点
?若存在,请求出此时点 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:①参加本次竞赛的学生共有100人;②第五组的百分比为16%;③成绩在70-80分的人数最多;④80分以上的学生有14名;其中正确的个数有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
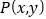 经过某种变换后得到点
经过某种变换后得到点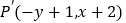 ,我们把点
,我们把点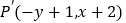 叫做点
叫做点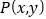 的终结点.已知点
的终结点.已知点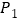 的终结点为
的终结点为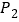 ,点
,点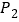 的终结点为
的终结点为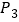 ,点
,点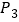 的终结点为
的终结点为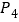 ,这样依次得到
,这样依次得到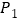 、
、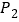 、
、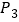 、
、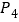 、…
、…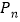 、…,若点
、…,若点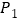 的坐标为
的坐标为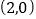 ,则点
,则点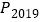 的坐标为__________.
的坐标为__________.
相关试题

