【题目】如图,在数轴上点![]() 表示的数是
表示的数是![]() 点
点![]() 在点
在点![]() 的右侧,且到点
的右侧,且到点![]() 的距离是18;点
的距离是18;点![]() 在点
在点![]() 与点
与点![]() 之间,且到点
之间,且到点![]() 的距离是到点
的距离是到点![]() 距离的2倍.
距离的2倍.
(1)点![]() 表示的数是____________;点
表示的数是____________;点![]() 表示的数是_________;
表示的数是_________;
(2)若点P从点![]() 出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为
出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动。设运动时间为![]() 秒,在运动过程中,当
秒,在运动过程中,当![]() 为何值时,点P与点Q之间的距离为6?
为何值时,点P与点Q之间的距离为6?
(3)在(2)的条件下,若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为![]() 在运动过程中,是否存在某一时刻使得
在运动过程中,是否存在某一时刻使得![]() ?若存在,请求出此时点
?若存在,请求出此时点![]() 表示的数;若不存在,请说明理由.
表示的数;若不存在,请说明理由.
![]()
![]()
参考答案:
【答案】(1)15, 3;(2)t=2或4;(3)1或![]()
【解析】
(1)利用数轴建立原点,再用AC和BC之间的关系即可求解;
(2)这里需要注意,存在2种情况使得P与点Q之间的距离为6,利用数轴将含t的表达式求解即可;
(3)先将PC+QB=4当做已知条件,再将PC和QB的算式代入求解即可.
(1)由题意可得:AB=18, A0=3(0为原点),
∴B0=AB-A0=15,
∵BC=2AC,
∴B0-0C=2(A0+0C),
∴0C=3.
故答案为:15, 3
(2)由题意可得:存在2种情况点P与点Q之间的距离为6,
①点P与点Q相遇前,18-6=(4+2)t ,则t=2秒;
②点P与点Q相遇后,18+6=(4+2)t ,则t=4秒.
故答案为:t=2或4.
(3)由题意可得:AC=6,PC=│6-4t│,QB=2t,
若PC+QB=4,
则│6-4t│+2t=4,
解得t=1或![]()
故答案为:点![]() 表示的数是1或
表示的数是1或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式的规律,解答下列问题:
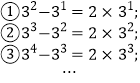
(1)按此规律,第④个等式为_________;第
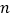 个等式为_______;(用含
个等式为_______;(用含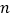 的代数式表示,
的代数式表示,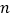 为正整数)
为正整数)(2)按此规律,计算:
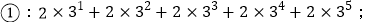
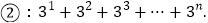
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,点D在CE上,AF⊥CB,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C、E分别为△ABD的边BD、AB上两点,且AE=AD,CE=CD,∠D=70゜,∠ECD=150゜,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M′、N′,则图中的全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
相关试题

