【题目】某汽车销售公司4月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该汽车的进价为30万元,每多售出1辆,所有售出汽车的进价均降低0.1万元/辆,月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)若该公司当月售出5辆汽车,则每辆汽车的进价为 万元.
(2)若汽车的售价为31万/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
参考答案:
【答案】(1)29.6;(2)需要销售 6 辆汽车.
【解析】
(1)根据若当月仅售出1辆汽车,则该辆汽车的进价为30万元,每多售出1辆,所有售出的汽车的进价均降低0.1万元/辆,得出该公司当月售出5辆汽车时,则每辆汽车的进价为:30-0.1×(5-1),即可得出答案;
(2)利用设需要售出x辆汽车,由题意可知,每辆汽车的销售利润,列出一元二次方程.
(1)若该公司当月售出5辆汽车,则每辆汽车的进价为:30-0.1×(5-1)=29.6万元.
故答案为:29.6;
(2)解:设需要销售 ![]() 辆,
辆,
则![]() ,
,
化简得 ![]() ,
,
![]() ,
,
![]() (舍去),
(舍去),
答:需要销售 6 辆汽车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个)
…
160
200
240
300
…
每个玩具的固定成本Q(元)
…
60
48
40
32
…
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
 (x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
(1)求直线l的函数解析式;
(2)过点P作直线l的垂线l1 , 交函数y= (x>0)图象于点C,求△OPC的面积.
(x>0)图象于点C,求△OPC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将
 沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC.
沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为 的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交  于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平面直角坐标系中,A(a,3)、B(b,6)、C(c,1),a、b、c都为实数,并且满足3b-5c=-2a-18,4b-c=3a+10
(1) 请直接用含a的代数式表示b和c
(2) 当实数a变化时,判断△ABC的面积是否发生变化?若不变,求其值;若变化,求其变化范围
(3) 当实数a变化时,若线段AB与y轴相交,线段OB与线段AC交于点P,且S△PAB>S△PBC,求实数a的取值范围.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 在直角坐标系第一象限内,
在直角坐标系第一象限内, 与
与 轴重合,
轴重合, ,
,
 ,
, ,点
,点 从点
从点 出发,以每秒
出发,以每秒 个单位向点
个单位向点 运动,点
运动,点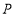 同时从点
同时从点 出发以每秒3个单位向点
出发以每秒3个单位向点 运动,当其中有一点到达终点时,另一点立即停止运动.
运动,当其中有一点到达终点时,另一点立即停止运动. 是射线
是射线 上的一点,且
上的一点,且 ,以
,以 为邻边作矩形
为邻边作矩形 .设运动时间为
.设运动时间为 秒.
秒.
(1)写出点
 的坐标( , );
的坐标( , ); ;
; .(用
.(用 的代数式表示)
的代数式表示)(2)当点
 落在
落在 上时,求此时
上时,求此时 的长?
的长?(3)①在
 的运动过程中,直角坐标系中是否存在点
的运动过程中,直角坐标系中是否存在点 ,使得
,使得 四点构成的四边形是菱形?若存在求出
四点构成的四边形是菱形?若存在求出 的值,不存在,请说明理由.
的值,不存在,请说明理由.②如图2,以
 为边按逆时针方向做正方形
为边按逆时针方向做正方形 ,当正方形
,当正方形 的顶点
的顶点 或
或 落在矩形
落在矩形 的某一边上时,则
的某一边上时,则 (直接写出答案).
(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的结论有_____个.

相关试题

