【题目】如图-1,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,E在线段AC上,连接AD,BE的延长线交AD于F.
(1)猜想线段BE,AD的数量关系和位置关系:________________________(不必证明);
(2)当点E为△ABC内部一点时,使点D和点E分别在AC的两侧,其它条件不变.
① 请你在图-2中补全图形;
②(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.

![]()
![]()
参考答案:
【答案】(1)BE=AD ;BE⊥AD;(2)①答案见解析;②成立
【解析】(1)先通过SAS证△BCE和△ACD全等,再根据全等三角形的性质即可得出BE,AD的数量关系和位置关系;
(2)按要求画图所,按(1)的证明思路即可进行证明.
解:(1)∵△ABC和△DEC都是等腰直角三角形,且∠ACB=∠DCE=90°,
∴BC=AC,CE=CD,
∴△BCE≌△ACD(SAS),
∴BE=AD , ![]()
∵![]()
∴![]()
∴BE⊥AD.
故答案为:BE=AD ,BE⊥AD.
(2)①如图
②(1)中结论仍然成立.
证明:∵△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,
∴BC=AC,EC=DC,
∵∠ACB=∠DCE=90°,
∴∠ACB ![]() =∠DCE
=∠DCE ![]() ,
,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
∵BC=AC,∠BCE=∠ACD,EC=DC,
∴△BCE≌△ACD(SAS),
∴ BE=AD,∠1=∠2,
∵∠3=∠4,
∴∠AFB=∠ACB=90°,
∴BE⊥AD.
-
科目: 来源: 题型:
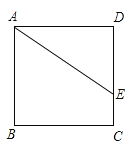
查看答案和解析>>【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,求F、C两点的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?

-
科目: 来源: 题型:
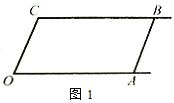
查看答案和解析>>【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
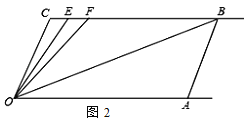
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.
-
科目: 来源: 题型:
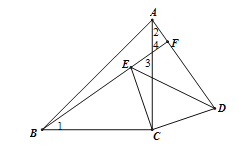
查看答案和解析>>【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系呢?
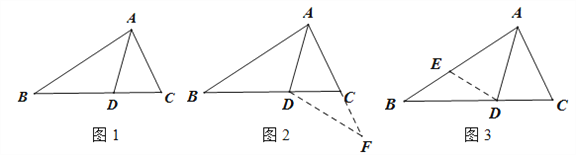
(1)通过观察、实验提出猜想:∠ACB与∠ABC的数量关系,用等式表示为: .
(2)小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:如图2,延长AC到F,使CF=CD,连接DF.通过三角形全等、三角形的性质等知识进行推理,就可以得到∠ACB与∠ABC的数量关系.
想法2:在AB上取一点E,使AE=AC,连接ED,通过三角形全等、三角形的性质等知识进行推理,就可以得到∠ACB与∠ABC的数量关系.
请你参考上面的想法,帮助小明证明猜想中∠ACB与∠ABC的数量关系(一种方法即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店二月份共销售各种水笔m支,三月份销售各种水笔的支数比二月份增长了10%,那么该文具店三月份共销售各种水笔________支.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=90°,∠AOB=30°,AB=2,△A′OB′可以看作是由△AOB绕点O逆时针旋转60°得到的,求点A′与点B的距离

相关试题

