搜索
【题目】某文具店二月份共销售各种水笔m支，三月份销售各种水笔的支数比二月份增长了10%，那么该文具店三月份共销售各种水笔________支．
参考答案：
【答案】1.1m
【解析】
根据题意可以求得三月份的销售量，从而可以解答本题．
解：由题意可得，
m(1＋10%)＝1.1m（支），
故答案为：1.1m．
-
科目： 来源： 题型：
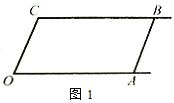
查看答案和解析>>【题目】如图1，已知射线CB∥OA，∠C=∠OAB，
（1）求证：AB∥OC；
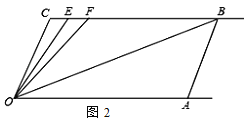
（2）如图2，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF.
①当∠C=110°时，求∠EOB的度数.
②若平行移动AB，那么∠OBC :∠OFC的值是否随之发生变化？若变化，找出变
化规律；若不变，求出这个比值.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图-1，△ABC和△DEC都是等腰直角三角形，∠ACB=∠DCE=90°，E在线段AC上，连接AD，BE的延长线交AD于F．
（1）猜想线段BE，AD的数量关系和位置关系：________________________（不必证明）；
（2）当点E为△ABC内部一点时，使点D和点E分别在AC的两侧，其它条件不变．
① 请你在图-2中补全图形；
②（1）中结论成立吗？若成立，请证明；若不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ABC中，AD是∠BAC的平分线，若AB=AC+CD，那么∠ACB与∠ABC有怎样的数量关系呢？
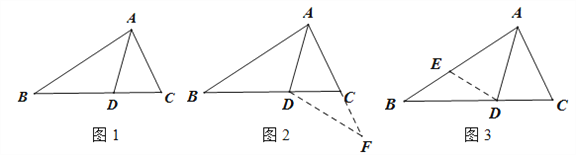
（1）通过观察、实验提出猜想：∠ACB与∠ABC的数量关系，用等式表示为： ．
（2）小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：
想法1：如图2，延长AC到F，使CF=CD，连接DF．通过三角形全等、三角形的性质等知识进行推理，就可以得到∠ACB与∠ABC的数量关系．
想法2：在AB上取一点E，使AE=AC，连接ED，通过三角形全等、三角形的性质等知识进行推理，就可以得到∠ACB与∠ABC的数量关系．
请你参考上面的想法，帮助小明证明猜想中∠ACB与∠ABC的数量关系（一种方法即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠A=90°，∠AOB=30°，AB=2，△A′OB′可以看作是由△AOB绕点O逆时针旋转60°得到的，求点A′与点B的距离
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场家电专柜购进一批甲，乙两种电器，甲种电器共用了10 350元，乙种电器共用了9 600元，甲种电器的件数是乙种电器的1.5倍，甲种电器每件的进价比乙种电器每件的进价少90元．
（1）甲、乙两种电器各购进多少件？
（2）商场购进两种电器后，按进价提高40%后标价销售，很快全部售完，求售完这批电器商场共获利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，将笔记本活页一角折过去，使角的顶点A落在
处，BC为折痕。（1）图①中，若∠1=30°，求∠
的度数；（2）如果又将活页的另一角斜折过去，使BD边与BA重合，折痕为BE，如图②所示，∠1=30°，求∠2以及∠
的度数；（3）如果在图②中改变∠1的大小，则
的位置也随之改变，那么问题（2）中∠
的大小是否改变？请说明理由。
相关试题
