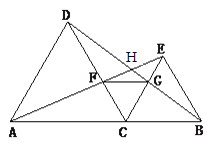
【题目】如图,C是线段AB上一点,分别以AC、CB为边作等边三角形ACD和CBE,连结AE、BD,AE交DC、DB分别为F点、H点,BD交CE于G点,连结FG.求证:① ∠FAC=∠HDC ;② ∠HFG=∠HAC;③ ∠BHA=120 °.
参考答案:
【答案】①证明见解析;②证明见解析;③证明见解析.
【解析】
①由“ASA”可证△ACE≌△DCB,从而可以证明∠FAC =∠HDC;
②先证明△ACF≌△DCG得CF=CG,得出△FCG是等边三角形得∠GFC=∠ACD,从而可证明FG∥AB,进而证明结论;
③证明∠DHA=∠ACD=60°即可得结论.
①∵△ACD和△BCE是等边三角形,
∴∠ACD=∠BCE=60°,AC=DC,EC=BC,
∴∠ACD+∠DCE=∠DCE+∠ECB,
即∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴∠FAC =∠HDC;
②∵∠EAC=∠BDC,
∵∠ACD=∠BCE=60°,
∴∠DCE=60°,
∴∠ACD=∠DCG=60°,且∠EAC=∠BDC,AC=DC,
∴△ACF≌△DCG(ASA),
∴CF=CG,
∵∠FCG=60°
∴△FCG是等边三角形
∴∠GFC=∠ACD=60°,
∴FG∥AB,
∴∠HFG=∠HAC
③∵△ACE≌△DCB
∴∠CAE=∠BDC
∵∠ACD=∠BDC+∠CBD=60°
∴∠DHA=∠CAE+∠CBD=60°
∴∠BHA=120 °.
-
科目: 来源: 题型:
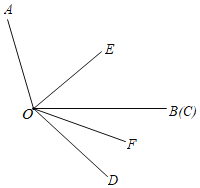
查看答案和解析>>【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C. 种D.
种D. 种
种 -
科目: 来源: 题型:
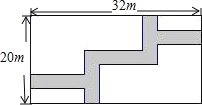
查看答案和解析>>【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用12 m长的一根铁丝围成长方形.
(1)如果长方形的面积为5
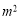 .那么此时长方形的长是多少?宽是多少?如果面积是8
.那么此时长方形的长是多少?宽是多少?如果面积是8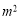 呢?
呢?(2)能否围成面积是10
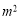 的长方形?为什么?
的长方形?为什么?(3)能围成的长方形的最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=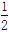 ,OB=4,OE=2.
,OB=4,OE=2.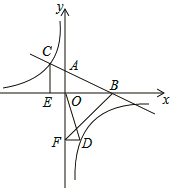
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=
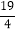 ,tan∠BAD=
,tan∠BAD=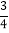 ,求⊙O的半径.
,求⊙O的半径.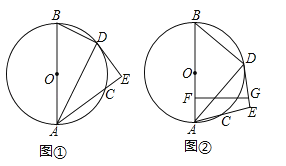
相关试题

