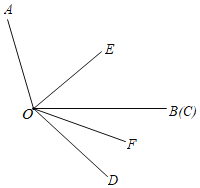
【题目】已知∠AOB=110°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.
(1)如图,求∠EOF的度数.
(2)如图,当OB、OC重合时,求∠AOE﹣∠BOF的值;
(3)当∠COD从图的位置绕点O以每秒3°的速度顺时针旋转t秒(0<t<10);在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化,若不发生变化,请求出该定值;若发生变化,请说明理由.
参考答案:
【答案】(1)∠EOF=75°;(2)∠AOE﹣∠BOF=35°;(3)∠AOE﹣∠BOF=35°.
【解析】
(1)直接利用角平分线的性质求出∠EOC和∠COF,相加即可求出答案;
(2)利用角平分线的性质求出∠AOE和∠COF,相减即可求出答案;
(3)当OC边绕O顺时针旋转时,∠AOB是变化的,∠AOB=110°+3°t,∠BOD是不变化的,所以∠AOE-∠BOF值是不变化的;
(1)∵OE平分∠AOC,OF平分∠BOD,
∴∠EOF=∠EOB+∠BOF=![]() ∠AOB+
∠AOB+![]() ∠BOD,
∠BOD,
∵∠AOB=110°,∠COD=40°,
∴∠EOF=75°;
(2)∵OE平分∠AOC,OF平分∠BOD,∠AOB=110°,∠COD=40°,
∴∠AOE=55°,∠BOF=20°,
∴∠AOE﹣∠BOF=35°;
(3)∵OF平分∠BOD,
∴∠BOF=![]() ∠BOD,
∠BOD,
∵∠AOB=110°,BO边绕点O以每秒3°的速度顺时针旋转t秒,
∴∠AOB=110°+3°t,∠BOF=![]() (40°+3°t),
(40°+3°t),
∴OE平分∠AOB,
∴∠AOE=![]() (110°+3°t),
(110°+3°t),
∴∠AOE﹣∠BOF=![]() (110°+3°t)﹣20°﹣
(110°+3°t)﹣20°﹣![]() t=35°,
t=35°,
∴在旋转过程中∠AOE﹣∠BOF的值是不会因t的变化而变化,∠AOE﹣∠BOF=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,甲、乙两种商品的进价和售价如表:
甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原售价销售,乙商品在原售价上打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
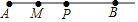
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y1=
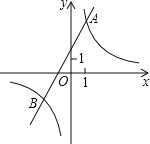
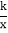 的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)
的图象与一次函数:y2=ax+b的图象相交于点A(1,4)、B(m,﹣2)(1)求出反比例函数和一次函数的关系式;
(2)观察图象,直按写出使得y1<y2成立的自变量x的取值范围;
(3)如果点C是x轴上的点,且△ABC的面积面积为6,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C. 种D.
种D. 种
种 -
科目: 来源: 题型:
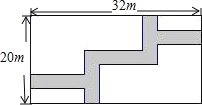
查看答案和解析>>【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
-
科目: 来源: 题型:
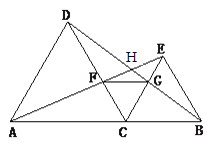
查看答案和解析>>【题目】如图,C是线段AB上一点,分别以AC、CB为边作等边三角形ACD和CBE,连结AE、BD,AE交DC、DB分别为F点、H点,BD交CE于G点,连结FG.求证:① ∠FAC=∠HDC ;② ∠HFG=∠HAC;③ ∠BHA=120 °.
相关试题

