【题目】用12 m长的一根铁丝围成长方形.
(1)如果长方形的面积为5![]() .那么此时长方形的长是多少?宽是多少?如果面积是8
.那么此时长方形的长是多少?宽是多少?如果面积是8![]() 呢?
呢?
(2)能否围成面积是10![]() 的长方形?为什么?
的长方形?为什么?
(3)能围成的长方形的最大面积是多少?
参考答案:
【答案】(1)当长方形的宽为![]() ,长为5
,长为5 ![]() 时,面积为
时,面积为![]() .当长方形的宽为
.当长方形的宽为![]() ,长为4
,长为4 ![]() 时,面积为8
时,面积为8 ![]() ;(2)不存在;(3)9
;(2)不存在;(3)9 ![]() .
.
【解析】
设长方形的宽为![]() ,而长方形的周长为12,由此得到长为
,而长方形的周长为12,由此得到长为![]() ,所以
,所以![]() ,进一步得
,进一步得![]() .
.
(1)由于长方形的面积为![]() ,由此列出方程
,由此列出方程![]() ,解方程即可求解;
,解方程即可求解;
(2)由于长方形的面积为 10 ![]() ,由此列出方程
,由此列出方程![]() ,判断方程的根的情况即可求解;
,判断方程的根的情况即可求解;
(3)设围成的长方形面积为![]() ,则有
,则有![]() .即
.即![]() ,要使该方程有解,必须判别式△
,要使该方程有解,必须判别式△![]() ,由此即可求出最大的
,由此即可求出最大的![]() 值解决问题.
值解决问题.
解:设长方形的宽为![]() 则长为
则长为![]() ,即为
,即为![]() ,则
,则![]() ,得
,得![]()
(1)根据题意,得![]() ,即
,即![]() ,
,![]() ,
,![]() (舍去).
(舍去).
![]() 当长方形的宽为
当长方形的宽为![]() ,长为
,长为![]()
![]() 时,面积为
时,面积为![]() .
.
同样,当面积为8 ![]() 时,有
时,有![]() ,即
,即![]() ,
,![]() ,
,![]() (舍去).
(舍去).
![]() 当长方形的宽为
当长方形的宽为![]() ,长为
,长为![]()
![]() 时,面积为8
时,面积为8 ![]() .
.
(2)当面积为10 ![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() ,故此方程无实数根.
,故此方程无实数根.
所以这样的长方形不存在.
(3)设围成的长方形面积为![]() ,则有
,则有![]() .即
.即![]() ,要使该方程有解,必须
,要使该方程有解,必须![]() ,即
,即![]()
![]() 最大的
最大的![]() 只能是9,即最大的面积为9
只能是9,即最大的面积为9 ![]() ,此时
,此时![]() ,
,![]() ,这时所围成的图形是正方形.
,这时所围成的图形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,若
,若 ,则还需添加的一个条件有( )
,则还需添加的一个条件有( )

A.
 种B.
种B. 种C.
种C. 种D.
种D. 种
种 -
科目: 来源: 题型:
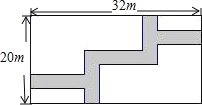
查看答案和解析>>【题目】如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽.
(部分参考数据:322=1024,522=2704,482=2304)
-
科目: 来源: 题型:
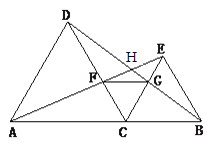
查看答案和解析>>【题目】如图,C是线段AB上一点,分别以AC、CB为边作等边三角形ACD和CBE,连结AE、BD,AE交DC、DB分别为F点、H点,BD交CE于G点,连结FG.求证:① ∠FAC=∠HDC ;② ∠HFG=∠HAC;③ ∠BHA=120 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=
 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=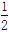 ,OB=4,OE=2.
,OB=4,OE=2.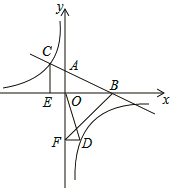
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是⊙O的直径,C是圆上一点,∠BAC的平分线交⊙O于点D,过D作DE⊥AC交AC的延长线于点E,如图①.
(1)求证:DE是⊙O的切线;
(2)若AB=10,AC=6,求BD的长;
(3)如图②,若F是OA中点,FG⊥OA交直线DE于点G,若FG=
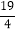 ,tan∠BAD=
,tan∠BAD=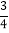 ,求⊙O的半径.
,求⊙O的半径.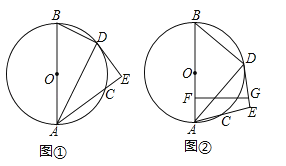
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017浙江省湖州市,第23题,10分)湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批淡水鱼放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为
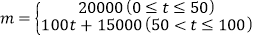 ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批淡水鱼放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

相关试题

