【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

参考答案:
【答案】(1)30°;(2)证明见解析.
【解析】
试题(1)利用“直角三角形的两个锐角互余”的性质和角平分的性质进行解答.
(2)由ASA证明△ACD≌△ECD来推知DA=DE.
试题解析:解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,∴∠CAB=60°.
又∵AD平分∠CAB,∴∠CAD=![]() ∠CAB=30°,即∠CAD=30°.
∠CAB=30°,即∠CAD=30°.
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°,∴∠ECD=90°. ∴∠ACD=∠ECD.
在△ACD与△ECD中,∵ ,∴△ACD≌△ECD(SAS).
,∴△ACD≌△ECD(SAS).
∴DA=DE.
-
科目: 来源: 题型:
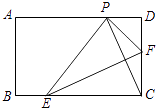
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=3,BC=5,点E、F是BC、CD边上的动点(包括端点处),若将纸片沿EF折叠,使得点C恰好落在AD边上点P处.设CF=x,则x的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为BC上一点,∠BAD=∠ABC,∠ADC=∠ACD,若∠BAC=63°,试求∠DAC、∠ADC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.
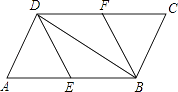
(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去新华书店,如图表示他离家的距离y(千米)与所用的时间s(小时)之间关系的函数图象
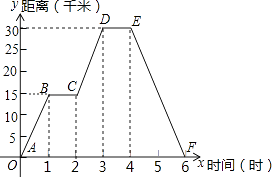
(1)根据图象回答:小明家离新华书店千米,小明用了小时到达新华书店;
(2)小明从家出发两个半小时走了千米;
(3)直线CD的函数解析式为;
(4)小明出发小时,离家12千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,顶点B的对应点是B′.
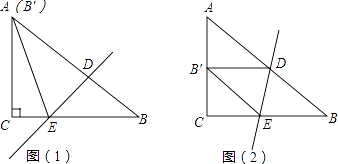
(1)如图(1),如果点B′和顶点A重合,求CE的长;
(2)如图(2),如果点B′和落在AC的中点上,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】固始县教体局举办”我的中国梦“为主题的知识竞赛,甲、乙两所学校参赛人数相等.比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并依据统计数据绘制了如下不完整的统计图表.
乙校成绩统计表分数(分)
70分
80分
90分
100分
人数(人)
7
1
8
(1)在图①中,“80分”所在扇形的圆心角度数为 .
(2)请你将图②补充完整.
(3)通过计算,说明哪所学校的学生成绩较整齐.
相关试题

