【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上述统计数据,把下面的图和表补充完整; 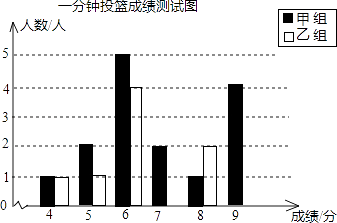
一分钟投篮成绩统计分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由. 
参考答案:
【答案】
(1)解:根据测试成绩表即可补全统计图(如图):
补全分析表:甲组平均分(4×1+5×2+6×5+7×2+8×1+9×4)÷15=6.8,
乙组中位数是第8个数,是7.
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 6.8 | 2.56 | 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 | 86.7% | 13.3% |
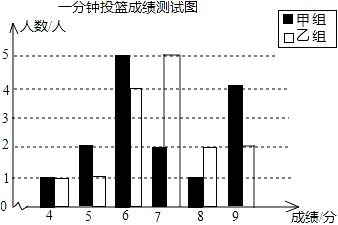
(2)解:甲乙两组平均数一样,乙组的方差低于甲组,说明乙组成绩比甲组稳定,又乙组合格率比甲组高,所以乙组成绩好于甲组
【解析】(1)根据测试成绩表求出乙组成绩为7分和9分的人数,补全统计图,再根据平均数的计算方法和中位数的定义求出平均数和中位数,即可补全分析表;(2)根据平均分、方差、中位数、合格率的意义即可写出支持小聪的观点的理由.
【考点精析】解答此题的关键在于理解频数分布直方图的相关知识,掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.
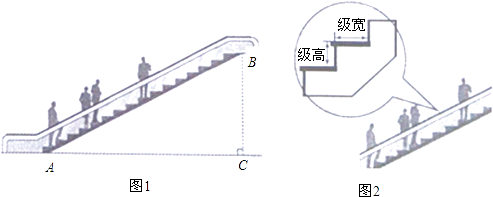
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,
, ,
, ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM. 求证:
求证: ;
; 求
求 的度数
的度数 用含
用含 的式子表示
的式子表示 ;
; 如图2,当
如图2,当 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断 的形状,并加以证明.
的形状,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= AB,求∠APB的度数.
AB,求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
-
科目: 来源: 题型:
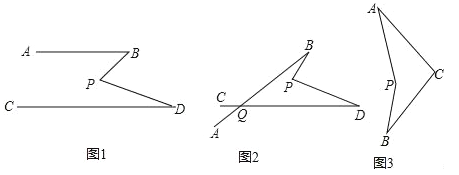
查看答案和解析>>【题目】(1)如图1,若AB∥CD,将点P在AB、CD内部,∠B,∠D,∠P满足的数量关系是 ,并说明理由.
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,利用(1)中的结论(可以直接套用),求∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?
(3)科技活动课上,雨轩同学制作了一个图(3)的“飞旋镖”,经测量发现∠PAC=30°,∠PBC=35°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
相关试题

