【题目】如图1,某超市从一楼到二楼的电梯AB的长为16.50米,坡角∠BAC为32°.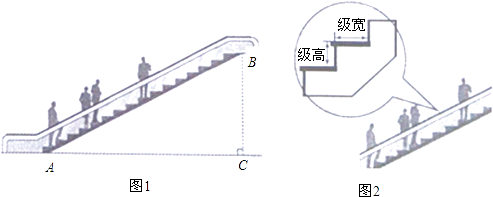
(1)求一楼与二楼之间的高度BC(精确到0.01米);
(2)电梯每级的水平级宽均是0.25米,如图2.小明跨上电梯时,该电梯以每秒上升2级的高度运行,10秒后他上升了多少米(精确到0.01米)?备用数据:sin32°=0.5299,cos32°=0.8480,tan32°=0.6249.
参考答案:
【答案】
(1)
解:sin∠BAC= ![]() ,
,
∴BC=AB×sin32°
=16.50×0.5299≈8.74米
(2)
解:∵tan32°= ![]() ,
,
∴级高=级宽×tan32°=0.25×0.6249=0.156225
∵10秒钟电梯上升了20级,
∴小明上升的高度为:20×0.156225≈3.12米
【解析】(1)在直角三角形ABC中利用∠BAC的正弦值和AB的长求得BC的长即可;(2)首先根据题意求得级高,然后根据10秒钟上升的级数求小明上升的高度即可.
【考点精析】认真审题,首先需要了解关于坡度坡角问题(坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 ,给出下列结论:
,给出下列结论:①
 是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;
是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的都为自然数的解有4对.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M. 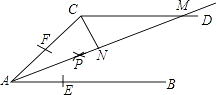
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是_____

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分)
4
5
6
7
8
9
甲组(人)
1
2
5
2
1
4
乙组(人)
1
1
4
5
2
2
(1)请你根据上述统计数据,把下面的图和表补充完整;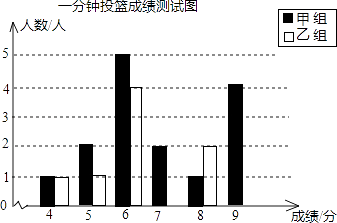
一分钟投篮成绩统计分析表:统计量
平均分
方差
中位数
合格率
优秀率
甲组
2.56
6
80.0%
26.7%
乙组
6.8
1.76
86.7%
13.3%
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,
, ,
, ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM. 求证:
求证: ;
; 求
求 的度数
的度数 用含
用含 的式子表示
的式子表示 ;
; 如图2,当
如图2,当 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断 的形状,并加以证明.
的形状,并加以证明.

相关试题

