【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一点Q,OB上有一点R,若△PQR周长最小,则最小周长是_____

参考答案:
【答案】12
【解析】
先画出图形,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△PQR=EF,再根据三角形各角之间的关系判断出△EOF的形状即可求解.
设∠POA=θ,则∠POB=30°-θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.
作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.
连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.

∵OA是PE的垂直平分线,
∴EQ=QP;
同理,OB是PF的垂直平分线,
∴FR=RP,
∴△PQR的周长=EF.
∵OE=OF=OP=12,且∠EOF=∠EOP+∠POF=2θ+2(30°-θ)=60°,
∴△EOF是正三角形,
∴EF=12,
即在保持OP=12的条件下△PQR的最小周长为12.
故答案为:12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=
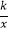 (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= 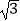 ,则k的值为 .
,则k的值为 . 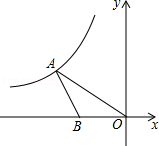
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动.设点P原来的速度为xcm/s.

(1)点Q的速度为 cm/s(用含x的代数式表示);
(2)求点P原来的速度.
(3)判断E点的位置并求线段DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,
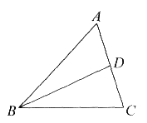
(1)作图:作BC边的垂直平分线分别交BC,BD于点E,F(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接CF,若∠A=60°,∠ABD=24°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(π﹣3)0﹣(﹣1)2017+(﹣
 )﹣2+tan60°+|
)﹣2+tan60°+|  ﹣2|
﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.

(1)求证:AD=DC;
(2)如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
相关试题

