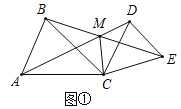
【题目】如图1,![]() ,
,![]() ,
,![]() ,AD、BE相交于点M,连接CM.
,AD、BE相交于点M,连接CM.![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数
的度数![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如图2,当
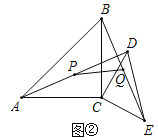
如图2,当![]() 时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断
时,点P、Q分别为AD、BE的中点,分别连接CP、CQ、PQ,判断![]() 的形状,并加以证明.
的形状,并加以证明.

参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 为等腰直角三角形,证明见解析.
为等腰直角三角形,证明见解析.
【解析】
分析(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
![]() 如图1,
如图1,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
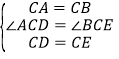 ,
,
![]() ≌
≌![]()
![]() ;
;
![]() 如图1,
如图1,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 中,
中,![]() ,
,
![]() ,
,
![]() 中,
中,![]() ;
;
![]() 为等腰直角三角形.
为等腰直角三角形.
证明:如图2,由![]() 可得,
可得,![]() ,
,
![]() ,BE的中点分别为点P、Q,
,BE的中点分别为点P、Q,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
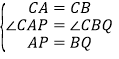 ,
,
![]() ≌
≌![]() ,
,
![]() ,且
,且![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等腰直角三角形.
为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
A. 21 B. 15 C. 9 D. 9或21
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.
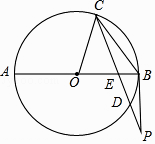
(1)求证:AEEB=CEED;
(2)若⊙O的半径为3,OE=2BE,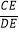 =
= 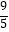 ,求tan∠OBC的值及DP的长.
,求tan∠OBC的值及DP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.
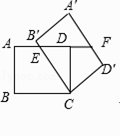
(1)如图①,当α=60°时,连接DD',求DD'和A'F的长;
(2)如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;
(3)如图③,当AE=EF时,连接AC,CF,求ACCF的值.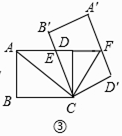
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=
 x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.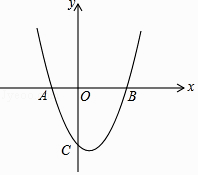
(1)求该抛物线的解析式;
(2)直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为 .求点H到OM'的距离d的值.
.求点H到OM'的距离d的值.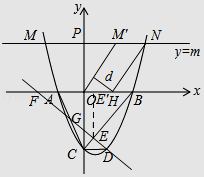
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度
,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为每秒1个单位长度,点N的运度为每秒2个单位长度 当点M第一次到达B点时,M、N同时停止运动.
当点M第一次到达B点时,M、N同时停止运动. 点M、N运动几秒后,M、N两点重合?
点M、N运动几秒后,M、N两点重合? 点M、N运动几秒后,可得到等边三角形
点M、N运动几秒后,可得到等边三角形 ?
? 当点M、N在BC边上运动时,能否得到以MN为底边的等腰
当点M、N在BC边上运动时,能否得到以MN为底边的等腰 ?如存在,请求出此时M、N运动的时间.
?如存在,请求出此时M、N运动的时间.
相关试题

