【题目】今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队及时联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣![]() x+m(m为常数).
x+m(m为常数).
(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.
(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].

参考答案:
【答案】(1)y=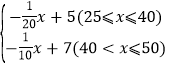 ;(2)45, 最大利润是45元.
;(2)45, 最大利润是45元.
【解析】试题分析:(1)把(40,3)代入y=-![]() x+m得,3=-
x+m得,3=-![]() ×40+m,求得y=-
×40+m,求得y=-![]() x+5,(25≤x≤40),设BC的解析式为:y=kx+b,把(40,3),(50,2)代入y=kx+b得得到y=-
x+5,(25≤x≤40),设BC的解析式为:y=kx+b,把(40,3),(50,2)代入y=kx+b得得到y=-![]() x+7,(40<x≤50);
x+7,(40<x≤50);
(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大,根据题意得到二次函数的解析式,求得当x=40时,W最大=30299元,当x=45时,W最大=32342.5元,即可得到结论.
(1)把(40,3)代入y=![]() x+m得,3=
x+m得,3=![]() ×40+m,
×40+m,
∴m=5,
∴y=![]() x+5,(25x40),
x+5,(25x40),
设BC的解析式为:y=kx+b,
把(40,3),(50,2)代入y=kx+b得,![]() ,
,
解得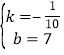 ,
,
∴y=110x+7,(40<x50),
综上所述:y=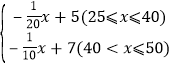 ;
;
(2)设该企业生产出的产品出厂价定为x元时,月利润W(元)最大,
根据题意得,W=(![]() x+5)(x20)32000=
x+5)(x20)32000=![]() x2+6x32100=120(x60)2+33900,
x2+6x32100=120(x60)2+33900,
∵25x40,
∴当x=40时,W最大=30299元,
W=(![]() x+7)(x20)32000=
x+7)(x20)32000=![]() x2+9x32140=
x2+9x32140=![]() (x45)+32342.5,
(x45)+32342.5,
∵40<x50,
∴当x=45时,W最大=32342.5元,
∵30299<32342.5,
∴当该企业生产出的产品出厂价定为45元时,月利润W(元)最大,最大利润是34342.5元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(操作发现)
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
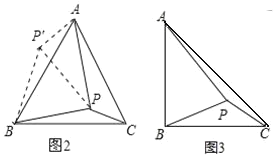
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=
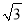 ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)①如图1,已知
 ,
,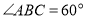 ,可得
,可得 __________.
__________.
②如图2,在①的条件下,如果
 平分
平分 ,则
,则 __________.
__________.
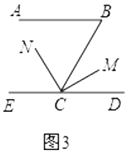
③如图3,在①、②的条件下,如果
 ,则
,则 __________.
__________.
(2)尝试解决下面问题:已知如图4,
 ,
, ,
,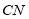 是
是 的平分线,
的平分线, ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出了(a+b)n (n=1,2,3,4,…)的展开式的系数规律(按n的次数由大到小的顺序):
1 1 (a+b)1=a+b
1 2 1 (a+b)2=a2+2ab+b2
1 3 3 1 (a+b)3=a3+3a2b+3ab2+b3
1 4 6 4 1 (a+b)4=a4+4a3b+6a2b2+4ab3+b4
…… ……
请依据上述规律,写出(x1)2019展开式中含x2018项的系数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上。

(1)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(2)若连接AA′、BB′,则这两条线段之间的关系是________________;
(3)在图中画出△ABC的高CD;
(4)△A′B′C′的面积为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)试探究△ABC的外接圆的圆心位置,并求出圆心坐标;
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
 B.
B.  C.
C.
 D.
D. 


相关试题

