【题目】如图,已知![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,且
,且![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]() .
.
【解析】试题分析:(1)已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,根据角平分线的性质定理可得CE=CF,再由![]() ,根据HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL证明Rt△AFC≌△Rt△AEC,即可得AE=AF,设DF=x,则有9+x=21-x,得x=6,在Rt△CDF中,根据勾股定理求得CF=8,在Rt△AFC中,再运用勾股定理求得AC即可.
,根据HL即可判定△BCE≌△DCF;(2)由Rt△BCE≌△Rt△DCF可得DF=EB,再由HL证明Rt△AFC≌△Rt△AEC,即可得AE=AF,设DF=x,则有9+x=21-x,得x=6,在Rt△CDF中,根据勾股定理求得CF=8,在Rt△AFC中,再运用勾股定理求得AC即可.
试题解析:
(![]() )证明:∵
)证明:∵![]() 平分
平分![]() ,
, ![]() 于
于![]() ,
, ![]() 于
于![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ≌
≌![]() .
.
(![]() )由(
)由(![]() )得,
)得, ![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 中,
中,
![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
设![]() ,则有
,则有![]() ,得
,得![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(
 )如图
)如图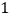 中,
中,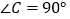 ,请用直尺和圆规作一条直线,把
,请用直尺和圆规作一条直线,把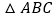 分割成两个等腰三角形(不写作法,但须保留作图痕迹).
分割成两个等腰三角形(不写作法,但须保留作图痕迹).(
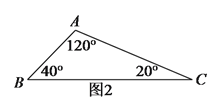
 )如图
)如图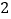 中,
中,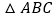 的三个内角分别为
的三个内角分别为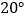 ,
, ,
,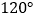 ,若
,若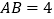 ,
,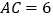 ,
,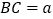 ,在
,在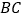 上找一个点
上找一个点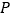 ,使
,使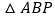 为等腰三角形,求出
为等腰三角形,求出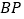 的长(可用含
的长(可用含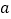 的代数式表示).
的代数式表示).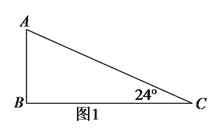


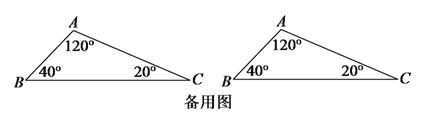
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, ,
, .
.(
 )如图,在平面直线坐标系中描出各点,并画出
)如图,在平面直线坐标系中描出各点,并画出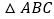 .
.(
 )请判断
)请判断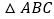 的形状,并说明理由.
的形状,并说明理由.(
 )把
)把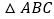 平移,使点
平移,使点 平移到点
平移到点 .作出
.作出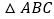 平移后的
平移后的 ,并直接写出
,并直接写出 中顶点
中顶点 的坐标为__________和平移的距离为__________.
的坐标为__________和平移的距离为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x2-3)2-12(x2-3)+36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明遇到一个问题:在
 中,
中, ,
,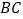 ,
, 三边的长分别为
三边的长分别为 、
、 、
、 ,求
,求 的面积.
的面积.小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为
 ),再在网格中画出格点
),再在网格中画出格点 (即
(即 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.参考小明解决问题的方法,完成下列问题:
(
 )图
)图 是一个
是一个 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为 ) .
) .①利用构图法在答卷的图
 中画出三边长分别为
中画出三边长分别为 、
、 、
、 的格点
的格点 .
. ②计算①中
 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)(
 )如图
)如图 ,已知
,已知 ,以
,以 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,连接
,连接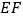 .
.①判断
 与
与 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.②若
 ,
, ,
, ,直接写出六边形
,直接写出六边形 的面积为__________.
的面积为__________.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 ,且
,且 .
.(
 )求证:
)求证: .
.(
 )若
)若 ,
, 于
于 ,
, 为
为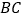 中点,
中点, 与
与 ,
, 分别交于点
分别交于点 ,
, .
.①判断线段
 与
与 相等吗?请说明理由.
相等吗?请说明理由.②求证:
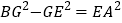 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种运算(a*b)=2a×(a+b),则4*5=。
相关试题

