【题目】如图,在平面直角坐标系中,有四边形![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() .
.


(1)求证:四边形![]() 是矩形;
是矩形;
(2)若反比例函数![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
(1)先求出AB,CD,BC,AD,AC的长,再根据勾股定理的逆定理得出∠ABC=90°,从而判断四边形ABCD是矩形;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,可得
,可得![]() ,求出直线BC解析式,设
,求出直线BC解析式,设![]() 为
为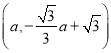 ,则
,则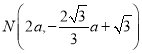 ,根据反比例函数图象上点的坐标特征列式求出a的值,得到点M的坐标即可求出k值.
,根据反比例函数图象上点的坐标特征列式求出a的值,得到点M的坐标即可求出k值.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
同理可得:![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵AC=3+1=4,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴四边形![]() 是矩形;
是矩形;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
设直线BC解析式为:![]() ,
,
代入![]() ,
,![]() 得:
得: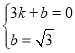 ,解得:
,解得: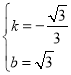 ,
,
∴直线![]() 解析式为:
解析式为:![]() ,
,
设![]() 为
为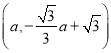 ,则
,则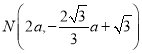 ,
,
∴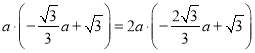 ,
,
解得:![]() ,
,
∴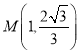 ,
,
∴![]() .
.
-
科目: 来源: 题型:
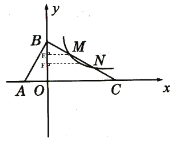
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=
 ,则四边形MABN的面积是( )
,则四边形MABN的面积是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 的三边为边分别向三角形外作正方形
的三边为边分别向三角形外作正方形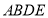 、
、 、
、 .连结
.连结 、
、 、
、 .若
.若 的面积是
的面积是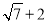 ,则以线段
,则以线段 、
、 、
、 为边的三角形的面积是__________.
为边的三角形的面积是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校为数学竞赛准备了若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为竞赛的奖品.若购买2支钢笔和3本笔记本需62元,购买5支钢笔和1本笔记本需90元.
(1)购买一支钢笔和一本笔记本各需多少钱?
(2)若学校准备购买钢笔和笔记本共80件奖品,并且购买的费用不超过1100元,则学校最多可以购买多少支钢笔?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,定点
 、
、 、
、 的坐标分别是(4,0)、(0,4)、(2,0),动点
的坐标分别是(4,0)、(0,4)、(2,0),动点 在第一象限,且到原点
在第一象限,且到原点 的距离为4个单位长度.
的距离为4个单位长度.(1)当点
 到两坐标轴的距离相等时,求
到两坐标轴的距离相等时,求 的面积;
的面积; (2)若点
 是线段
是线段 (不与点
(不与点 、
、 重合)上的动点,当
重合)上的动点,当 是等腰直角三角形时,求点
是等腰直角三角形时,求点 到
到 轴的距离.
轴的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
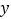 的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
A.abc<0
B.b=2a
C.a+b+c=0
D.2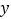
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图一,在△ABC中,AD是角平分线,AE是高,∠ABC=30°,∠ACB=70°.
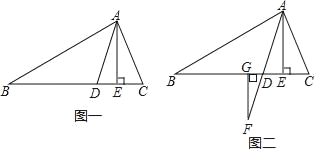
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
相关试题

