【题目】已知如图一,在△ABC中,AD是角平分线,AE是高,∠ABC=30°,∠ACB=70°.
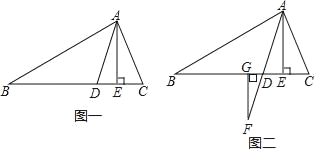
(1)求∠DAE的度数.
(2)如图二,若点F为AD延长线上一点,过点F作FG⊥BC于点G,求∠AFG的度数.
参考答案:
【答案】(1)∠DAE=20°;(2)∠AFG=20°.
【解析】
(1)先利用三角形内角和定理求出∠BAC=80°,再利用角平分线求出∠BAD=40°,进而求出∠ADC=∠BAD+∠ABD=70°,最后用三角形的内角和定理 即可得出结论;
(2)先判断出FG∥AE,即可得出结论.
(1)在△ABC中,
∵∠ABC=30°,∠ACB=70°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣30°﹣70°=80°
∵AD平分∠BAC
∴∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() ×80°=40°,
×80°=40°,
在△ABD中,
∠ADC=∠BAD+∠ABD=40°+30°=70°
∵AE为三角形的高,
∴∠AED=90°.
在△AED中,
∠DAE=180°﹣∠ADE﹣∠AED=180°﹣70°﹣90°=20°.
(2)∵FG⊥BC∴∠FGD=90°
∵∠AED=90°
∴∠FGD=∠AED
∴FG∥AE
∴∠AFG=∠DAE
由(1)可知∠DAE=20°
∴∠AFG=20°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有四边形
 ,且
,且 ,
, ,
, ,
, .
.

(1)求证:四边形
 是矩形;
是矩形;(2)若反比例函数
 与
与 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,定点
 、
、 、
、 的坐标分别是(4,0)、(0,4)、(2,0),动点
的坐标分别是(4,0)、(0,4)、(2,0),动点 在第一象限,且到原点
在第一象限,且到原点 的距离为4个单位长度.
的距离为4个单位长度.(1)当点
 到两坐标轴的距离相等时,求
到两坐标轴的距离相等时,求 的面积;
的面积; (2)若点
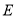 是线段
是线段 (不与点
(不与点 、
、 重合)上的动点,当
重合)上的动点,当 是等腰直角三角形时,求点
是等腰直角三角形时,求点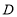 到
到 轴的距离.
轴的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
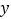 的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
A.abc<0
B.b=2a
C.a+b+c=0
D.2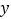
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB切⊙O于A、B,
 ,点C是⊙O上异于A、B的任意一点,则
,点C是⊙O上异于A、B的任意一点,则  = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来随着全国楼市的降温,商品房的价格开始呈现下降趋势,2012年某楼盘平均售价为5000元/平方米,2014年该楼盘平均售价为4050元/平方米.
(1)如果该楼盘2013年和2014年楼价平均下降率相同,求该楼价的平均下降率;
(2)按照(1)中楼价的下降速度,请你预测该楼盘2015年楼价平均是多少元/平方米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.

相关试题

