【题目】尝试探究并解答:
(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为 ;若x=2,则这个代数式的值为 ,可见,这个代数式的值因x的取值不同而 (填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子,我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式同样地,把一个多项式进行部分因式分解可以解决代数式的最大(或最小)值问题例如:x2+2x+3=(x2+2x+1)+2=(x+1)2+2,因为(x+1)2≥0,所以(x+1)2+2≥2,所以这个代数式x2+2x+3有最小值是2,这时相应的x的值是 .
(3)猜想:①4x2﹣12x+13的最小值是 ;
②﹣x2﹣2x+3有 值(填“最大”或“最小”).
参考答案:
【答案】(1)6,11,变化;(2)﹣1;(3)①4;②最大.
【解析】
(1)把x的值代入计算即可.
(2)根据非负数的性质即可解决问题.
(3)利用配方法即可解决问题.
(1)当x=1时,x2+2x+3=1+2+3=6.
当x=2时,x2+2x+3=4+4+3=11,这个代数式的值因x的取值不同而变化.
故答案为:6,11,变化.
(2)∵x2+2x+3=(x2+2x+1)+2=(x+1)2+2,∴当x=﹣1时,这个代数式的值的最小值为2.
故答案分别为:﹣1.
(3)①∵4x2﹣12x+13=4(x﹣![]() )2+4,∴x=
)2+4,∴x=![]() 时,代数式的最小值为4;
时,代数式的最小值为4;
②∵﹣x2﹣2x+3=﹣(x+1)2+4,∴x=﹣1时,代数式的最大值为4.
故答案为:4,最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的
 ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 
-
科目: 来源: 题型:
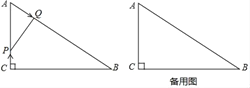
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,AB=6m,点P在线段AC上以1cm/s的速度由点C向点A运动,同时,点Q在线段AB上以2cm/s的速度由点A向点B运动,设运动时间为t(s).
(1)当t=1时,判断△APQ的形状,并说明理由;
(2)当t为何值时,△APQ与△CQP全等?请写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
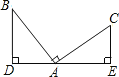
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
-
科目: 来源: 题型:
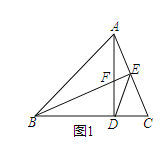
查看答案和解析>>【题目】如图1,在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。求证:ED平分∠FEC。
-
科目: 来源: 题型:
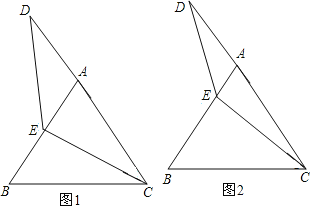
查看答案和解析>>【题目】等边△ABC中,点E在AB上,点D在CA的延长线上,且ED=EC.试探索以下问题:
(1)如图1,当E为AB中点时,试确定线段AD与BE的大小关系,请你直接写出结论:AD BE;
(2)如图2,若点E为线段AB上任意一点,(1)中结论是否成立,若成立,请证明结论,若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则下列结论错误的是( )
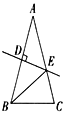
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
相关试题

