Question

【题目】如图，在△ABC中，AB=5，AD=4，BD=DC=3，且DE⊥AB于E，DF⊥AC于点F．

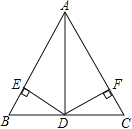
（1）请写出与A点有关的三个正确结论；

（2）DE与DF在数量上有何关系？并给出证明．

Answer 1

【答案】①AD⊥BC，②AD平分∠BAC，③AB=AC，④△ABE是等腰三角形，⑤△AED≌△AFD；（2） DE=DF．证明详见解析．

【解析】

（1）先运用勾股定理的逆定理证明△ABD为直角三角形，且∠ADB=90°，再运用勾股定理求出AC=5，则AB=AC，然后利用等腰三角形的性质即可求解；

（2）根据角平分线的性质即可得出DE=DF．

（1）AD⊥BC，∠BAD=∠CAD，AB=AC等．理由如下：

∵AB=5，AD=4，BD=3，

∴42+32=52．

∴△ABD为直角三角形，且∠ADB=90°．

∵CD=3，

∴AC=，

∴AB=AC，

又∵BD=CD，

∴AD⊥BC，∠BAD=∠CAD；

（2）DE=DF，理由如下：

∵∠BAD=∠CAD，DE⊥AB于E，DF⊥AC于点F，

∴DE=DF．