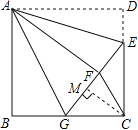
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.

(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
参考答案:
【答案】(1)①证明详见解析;②3;(2)![]() .
.
【解析】试题分析:(1)①利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
②利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;
(2)首先过C作CM⊥GF于M,由勾股定理以及由面积法得,CM=2.4,进而得出答案
解:(1)①在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
![]() ,
,
∴△ABG≌△AFG(HL);
②∵CD=3DE
∴DE=2,CE=4,
设BG=x,则CG=6﹣x,GE=x+2
∵GE2=CG2+CE2
∴(x+2)2=(6﹣x)2+42,
解得x=3,
∴CG=6﹣3=3;
(2)如图,过C作CM⊥GF于M,
∵BG=GF=3,
∴CG=3,EC=6﹣2=4,
∴GE=![]() =5,
=5,
CMGE=GCEC,
∴CM×5=3×4,
∴CM=2.4,
∴S△FGC=GF×CM=×3×2.4=3.6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AD=4,BD=DC=3,且DE⊥AB于E,DF⊥AC于点F.
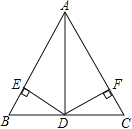
(1)请写出与A点有关的三个正确结论;
(2)DE与DF在数量上有何关系?并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,求C′B的长度.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,求C′B的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店准备销售甲、乙两种商品共80件,已知甲种商品进货价为每件70元,乙种商品进货价为每件35元,在定价销售时,2件甲种商品与3件乙种商品的售价相同,3件甲种商品比2件乙商品的售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
(3)若这批商品全部售完,该商店至少盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王上周五在股市上以收盘价(收市时的价格)每股25元买进某公司股票1 000股,在接下来的一周交易日内,小王记下该股票每日收盘价相比前一天的涨跌情况:(单位:元)

根据上表回答问题:
(1)星期二收盘时,该股票每股______元.
(2)本周内股票收盘时的最高价______元.
(3)已知买入股票与卖出股票均需支付成交金额的千分之五的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )

A.2+
 B.
B. C.
C. D.3
D.3
相关试题

