【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.
![]()
参考答案:
【答案】7 2或4 1 ﹣2.5或4.5.
【解析】
(1)先求出![]() 的结果,再求出它的绝对值即可;
的结果,再求出它的绝对值即可;
(2)根据绝对值的性质得到![]() ,解方程即可求解;
,解方程即可求解;
(3)根据绝对值的意义,可知![]() 是数轴上表示数x的点与表示数3的点之间的距离,
是数轴上表示数x的点与表示数3的点之间的距离,![]() 是数轴上表示数x的点与表示数﹣1的点之间的距离,若
是数轴上表示数x的点与表示数﹣1的点之间的距离,若![]() ,则此点必在
,则此点必在![]() 与
与![]() 之间,故
之间,故![]() ,
,![]() ,由此可得到关于x的方程,求出x的值即可;
,由此可得到关于x的方程,求出x的值即可;
(4)由于![]() 及
及![]() 的符号不能确定,故应分
的符号不能确定,故应分![]() ,
,![]() ,
,![]() 三种情况解答.
三种情况解答.
解:(1)![]() 的值为7;
的值为7;
(2)∵![]() ,
,
∴![]() ,
,
解得x=2或4.
故x的值为2或4;
(3)根据绝对值的意义可知,此点必在![]() 与3之间,故
与3之间,故![]() ,
,![]() ,
,
∴原式可化为![]() ,
,
∴x=1.
故x的值为1;
(4)在数轴上3和![]() 的距离为4,则满足方程的x的对应点在
的距离为4,则满足方程的x的对应点在![]() 的左边或3的右边.
的左边或3的右边.
若x的对应点在![]() 的左边,则
的左边,则![]() ;
;
若x的对应点在3的右边,则![]() .
.
所以原方程的解是![]() 或x=4.5.
或x=4.5.
故x的值为![]() 或4.5.
或4.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接
 交AD于F点.
交AD于F点.(1)若
 ,如图,
,如图,①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当
 时,
时, ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取 E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1:
 :3,求∠AED的度数;
:3,求∠AED的度数;(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=
 ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
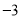
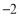
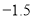
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
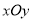 中,记
中,记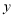 与
与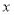 的函数
的函数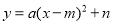 (
(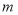 ≠0,n≠0)的图象为图形G, 已知图形G与
≠0,n≠0)的图象为图形G, 已知图形G与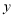 轴交于点
轴交于点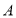 ,当
,当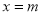 时,函数
时,函数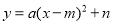 有最小(或最大)值n, 点B的坐标为(
有最小(或最大)值n, 点B的坐标为(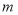 ,
, 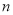 ),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
),点A、B关于原点O的对称点分别为C、D,若A、B、C、D中任何三点都不在一直线上,且对角线AC,BD的交点与原点O重合,则称四边形ABCD为图形G的伴随四边形,直线AB为图形G的伴随直线.
(1)如图,若函数
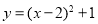 的图象记为图形G,求图形G的伴随直线的表达式;
的图象记为图形G,求图形G的伴随直线的表达式;(2)如图,若图形G的伴随直线的表达式是
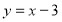 ,且伴随四边形的面积为12,求
,且伴随四边形的面积为12,求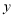 与
与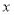 的函数
的函数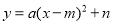 (m>0,n <0)的表达式;
(m>0,n <0)的表达式;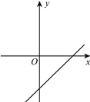
(3)如图,若图形G的伴随直线是
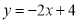 ,且伴随四边形ABCD是矩形,求点B的坐标.
,且伴随四边形ABCD是矩形,求点B的坐标.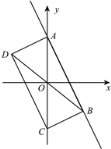
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会干部对校学生会倡导的“牵手特殊教育”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).己知A、B两组捐款人数的比为1: 5.
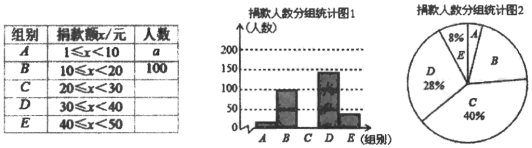
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”
(3)根据统计情况,估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.
-
科目: 来源: 题型:
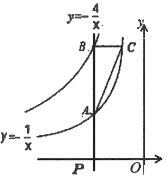
查看答案和解析>>【题目】如图,点
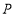 为
为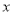 轴负半轴上的一个点,过点
轴负半轴上的一个点,过点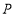 作
作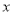 轴的垂线,交函数
轴的垂线,交函数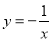 的图像于点
的图像于点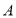 ,交函数
,交函数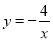 的图像于点
的图像于点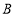 ,过点
,过点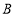 作
作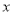 轴的平行线,交
轴的平行线,交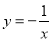 于点
于点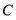 ,连接
,连接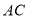 .
.
(1)当点
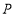 的坐标为(–1,0)时,求
的坐标为(–1,0)时,求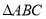 的面积;
的面积;(2)若
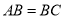 ,求点
,求点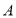 的坐标;
的坐标;(3)连接
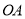 和
和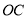 .当点
.当点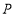 的坐标为(
的坐标为(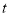 ,0)时,
,0)时,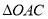 的面积是否随
的面积是否随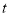 的值的变化而变化?请说明理由.
的值的变化而变化?请说明理由.
相关试题

