【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

参考答案:
【答案】(1)①见解析② FM=FC(2)CE=![]() AF
AF
【解析】
(1)①按要求画图即可;②根据“AAS”证明△AFM≌△DFC,即可证明结论成立;
(2)过点M作![]() ∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得
∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得![]() .再证明∠FHA=90°,根据勾股定理得出
.再证明∠FHA=90°,根据勾股定理得出![]() ,进而可求出线段CE与AF的数量关系.
,进而可求出线段CE与AF的数量关系.
(1)①如图,
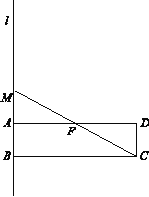
② FM=FC.
∵点B关于AD的对称点为M,
∴AB=AM.
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AM=CD.
∵![]() ,
,
∴四边形ABCD是矩形,
∴∠MAF=∠CDF,
又∵∠AFM=∠CFD,
∴△AFM≌△DFC,
∴FM=FC;
(2)CE与AF的数量关系是CE=![]() AF
AF
证明:过点M作![]() ∥CD交AD于点G.
∥CD交AD于点G.
∵B,M关于AD对称,
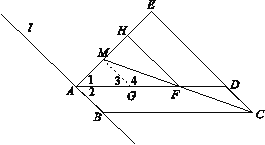
∴∠1=∠2,AB=AM.
∵四边形ABCD为平行四边形
∴AB∥CD.
∵MG∥CD,
∴MG∥AB.
∴∠2=∠3.
∴∠1=∠3.
∴AM=MG.
∵AB=AM,AB=CD,
∴MG=CD.
∵MG∥CD,
∴ ∠4=∠FDC.
∵∠MFG=∠CFD,
∴ △MFG≌ △CFD.
∴ FM=FC.
∴F为CM的中点,
∵H为ME的中点,
∴ FH∥CE,
![]()
∵∠ABC=135°, 平行四边形ABCD中,AD∥BC,
∴∠2=180°-∠ABC=45°.
∴由对称性,∠1=∠2=45°.
∵FH∥CD,AB∥CD,
∴FH∥AB.
∴∠HFA=∠2=45°.
∴∠FHA=90°,HA=HF.
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
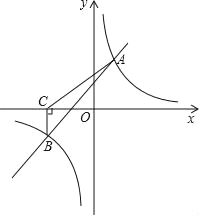
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
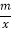 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>
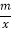 的解集;
的解集;(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级共有200名学生.为了解该年级学生A课程的学习情况,从中随机抽取40名学生进行测试(测试成绩是百分制,且均为正整数), 并对数据(A课程测试成绩)进行整理、描述和分析.这组数据(A课程测试成绩)的平均分数是78.38. 下表是随机抽取的40名学生A课程测试成绩频数分布表
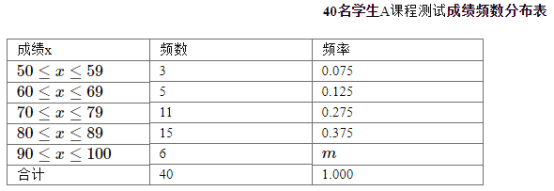
根据以上信息,回答下列问题:
(1)写出表中
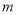 的值;
的值;(2)80分及以上的频数之和是21,79分及以下的频数之和是19,而平均分数(78.38)在80分以下. 由此可知,这次测验的成绩高于平均分的人数________(填“多”或“少”),低于平均分的人数________(填“多”或“少”),成绩属偏________(填“高”或“低”)分布;
(3)假设该年级学生都参加此次测试,估计这次A课程测试成绩90分及以上的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数 的图象与性质进行了探究.
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数
 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)下表是y与x的几组对应值.
x
…
-3
-2
-1

1
2
3
4
5
…
y
…




3



m
…
求m的值;
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1:
 :3,求∠AED的度数;
:3,求∠AED的度数;(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=
 ,求CN的长.
,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克)
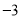
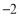
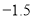
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.

相关试题

