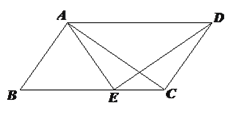
【题目】如图,在四边形ABCD中,AB//CD,∠B=∠ADC,点E是BC边上的一点,且AE=DC.
(1)求证:△ABC≌△EAD ;
(2)如果AB⊥AC,求证:∠BAE= 2∠ACB.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)易证△ABC≌△CDA得BC=AD,AB=DC,∠ACB=∠CAD;再证∠B=∠EAD;进而再证明AB=AE,即可得证;
(2)过点A作AH⊥BC于H ,利用等腰三角形的三线合一的性质和直角三角形两锐角互余即可得证.
试题解析:(1)∵ AB//CD,
∴ ∠BAC=∠DCA .
又 ∠B=∠ADC,AC=CA,
∴ △ABC≌△CDA .
∴ BC=AD,AB=DC,∠ACB=∠CAD .
又 AE=DC,AB=DC,
∴ AB=AE .
∴ ∠B=∠AEB .
又 ∠ACB=∠CAD,
∴ AD//BC,
∴ ∠AEB=∠EAD .
∴ ∠B=∠EAD .
在△ABC与△EAD中,
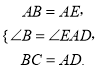
∴ △ABC≌△EAD .
(2)过点A作AH⊥BC于H .

∵ AB=AE,AH⊥BC .
∴ ∠BAE=2∠BAH .
在△ABC中,
∵ ∠BAC+∠B+∠ACB=180°,
又 AB⊥AC,∴ ∠BAC=90°.
∴ ∠B+∠ACB=90°.
同理:∠B+∠BAH=90°.
∴ ∠BAH=∠ACB .
∴ ∠BAE=2∠ACB .
-
科目: 来源: 题型:
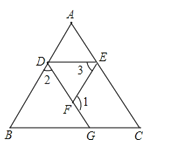
查看答案和解析>>【题目】如图,已知∠1+∠2=180°,∠B=∠3,你能判断∠C与∠AED的大小关系吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】截至北京时间2020年5月7日6:30,全球累计新冠肺炎确诊病例超过3 740 000例,3 740 000用科学记数法可表示为( )
A.374×104B.37.4 ×105C.3.74×106D.0.374×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.±0.3是0.09的平方根,即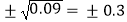
B.存在立方根和平方根相等的数
C.正数的两个平方根的积为负数
D.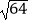 的平方根是±8
的平方根是±8 -
科目: 来源: 题型:
查看答案和解析>>【题目】实验中学为了鼓励同学们参加体育锻炼,决定为每个班级配备排球或足球一个,已知一个排球和两个足球需要140元,两个排球和一个足球需要230元.
(1)求排球和足球的单价.
(2)全校共有50个班,学校准备拿出不超过2400元购买这批排球和足球,并且要保证排球的数量不超过足球数量的
 ,问:学校共有几种购买方案?哪种购买方案总费用最低?
,问:学校共有几种购买方案?哪种购买方案总费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】-a-(b-c)去括号应为( )
A. -a+b+c B. -a+b-c C. -a-b-c D. -a-b+c
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年第九届贵阳国际汽车展览会暨新能源智能汽车展于4月18日—22日在贵阳国际会议展览中心举行,据统计,这五天共销售各种车辆约350万台,350万这个数用科学记数法表示为( )
A.3.5×105.B.35×105.C.3.5×106.D.0.35×107.
相关试题

