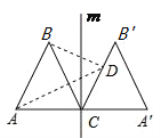
【题目】如图,等边三角形△ABC的边长为4,过点C的直线![]() ⊥AC,且△ABC与△A′B′C关于直线
⊥AC,且△ABC与△A′B′C关于直线![]() 对称,D为线段BC′上一动点,则AD+BD的最小值是______;
对称,D为线段BC′上一动点,则AD+BD的最小值是______;
参考答案:
【答案】8
【解析】连接BB/,根据△ABC、△A/CB/均为正三角形即可得出A/CBB/为菱形,进而得出点B关于CB/对称的点A/,以此确定点D与点C重合时,AD+BD的最小,代入数据即可得出结论.
解:连接BB/,如图所示.
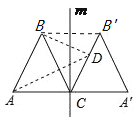
∵△ABC、△A/CB/ /均为正三角形,
∴∠ACB=∠A/=60°,A/C=BC=A/B/,
∴A/B/∥BC,
∴四边形A/CBB/ /为菱形,
∴点B关于CB/对称的点A/,
∴当点D与点C重合时,AD+BD取最小值,
此时AD+BD=4+4=8.
故答案为:8.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质,找出点B关于CB/对称的点A/是解题的关键.
-
科目: 来源: 题型:
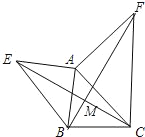
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.试判断线段EC与BF的关系并证明.
-
科目: 来源: 题型:
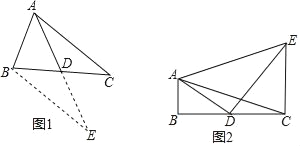
查看答案和解析>>【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=8,AC=6,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,再证明“△ADC≌△EDB”.
(1)探究得出AD的取值范围是_____;
(2)(问题解决)如图2,△ABC中,∠B=90°,AB=2,AD是△ABC的中线,CE⊥BC,CE=4,且∠ADE=90°,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
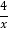 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=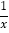 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.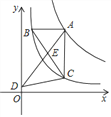
-
科目: 来源: 题型:
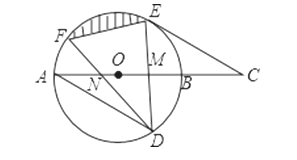
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
(1)求⊙O的半径;
(2)求证:CE是⊙O的切线;
(3)若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣41)+(+28)+(﹣59)+(+72);
(2)(﹣0.5)+(﹣3
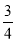 )+2.75+(+7
)+2.75+(+7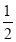 );
);(3)12﹣(﹣8)﹣(+6)﹣13;
(4)(+6.2)﹣(+4.6)﹣(﹣3.6)﹣(﹣2.8)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,山坡AB的坡度i=1:
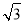 ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据: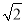 ≈1.414,
≈1.414,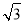 ≈1.732)
≈1.732)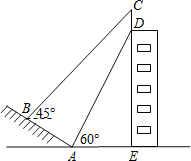
相关试题

