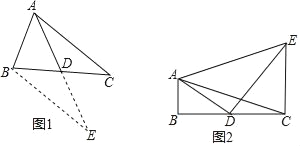
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在△ABC中,AB=8,AC=6,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,再证明“△ADC≌△EDB”.
(1)探究得出AD的取值范围是_____;
(2)(问题解决)如图2,△ABC中,∠B=90°,AB=2,AD是△ABC的中线,CE⊥BC,CE=4,且∠ADE=90°,求AE的长.
参考答案:
【答案】(1)1<AD<7;(2)AE=6
【解析】
(1)根据全等三角形的性质、三角形的三边关系计算;
(2)延长AD交EC的延长线于F,证明△ABD≌△FCD,根据全等三角形的性质解答.
(1)∵△ADC≌△EDB,
∴BE=AC=6,
8-6<AE<8+6,
∴1<AD<7,
故答案为:1<AD<7;
(2)延长AD交EC的延长线于F,
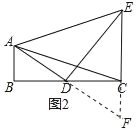
∵AB⊥BC,EF⊥BC,
∴∠ABD=∠FCD,
在△ABD和△FCD中,
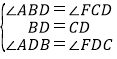 ,
,
∴△ABD≌△FCD,
∴CF=AB=2,AD=DF,∵∠ADE=90°,∴AE=EF,
∵EF=CE+CF=CE+AB=4+2=6,
∴AE=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )

A. 15 B. 12.5 C. 14.5 D. 17
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.试判断线段EC与BF的关系并证明.
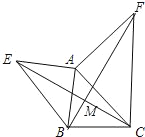
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若点B,P在直线a的异侧,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.
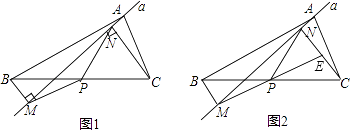
(1)延长MP交CN于点E(如图2).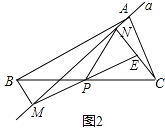
①求证:△BPM≌△CPE;
②求证:PM=PN;
(2)若直线a绕点A旋转到图3的位置时,点B,P在直线a的同侧,其它条件不变,此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;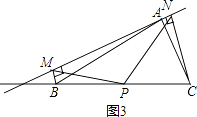
(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变,请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线y=x2﹣2mx+m2﹣9.
(1)求证:无论m为何值,该抛物线与x轴总有两个交点;
(2)该抛物线与x轴交于A,B两点,点A在点B的左侧,且OA<OB,与y轴的交点坐标为(0,﹣5),求此抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与x轴的交点为N,若点M是线段AN上的任意一点,过点M作直线MC⊥x轴,交抛物线于点C,记点C关于抛物线对称轴的对称点为D,点P是线段MC上一点,且满足MP= MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由.
MC,连结CD,PD,作PE⊥PD交x轴于点E,问是否存在这样的点E,使得PE=PD?若存在,求出点E的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,若点A(﹣1,y1)、B(﹣6,y2)是它图象上的两点,则y1与y2的大小关系是( )
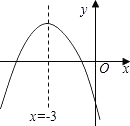
A.y1<y2
B.y1=y2
C.y1>y2
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是( )
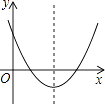
A.a>0
B.c>0
C.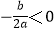
D.b2+4ac>0
相关试题

