搜索
【题目】一只小虫子落在数轴上的某点
，第一次从
向左跳一个单位到
，第二次从向右跳
个单位到
，第三次从向左跳
个单位到
，第四次从向右跳
个单位到
，按以上规律跳了
次时，它落在数轴上的点
所表示的数恰好是2019，则这只小虫的初始位置所在的数是_____．
参考答案：
【答案】1969
【解析】
根据数轴上的点的移动规律：“左减右加”可分别用P0表示出P1、P2、P3，……，根据规律可表示出P100，由点
所表示的数恰好是2019即可求出P0表示的数，可得答案．
P1=P0-1，
P2=P1+2=P0-1+2，
P3=P2-3=P0-1+2-3，
……
P100=P0-1+2-3+4-……-99+100=P0+50，
∵点所表示的数恰好是2019，
∴P0=2019-50=1969，
∴这只小虫的初始位置
所在的数是1969，
故答案为：1969
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线AB∥CD，直线EF与AB，CD分别相交于点E，F．
（1）如图1，若∠1=60°，求∠2=__________；∠3=__________．
（2）若点P是平面内的一个动点，连结PE，PF，探索∠EPF，∠PEB，∠PFD三个角之间的关系．
①当点P在图2的位置时，可得∠EPF=∠PEB+∠PFD． 理由如下：
如图2，过点P作MN∥AB，则∠EPM=∠PEB（__________）
∵AB∥CD（已知） MN∥AB（作图）
∴MN∥CD（__________）
∴∠MPF=∠PFD （__________）
∴__________+__________=∠PEB+∠PFD（等式的性质）
即：∠EPF=∠PEB+∠PFD．请补充完整说理过程（填写理由或数学式）
②当点P在图3的位置时，此时∠EPF=80°，∠PEB=156°，则∠PFD=__________；
③当点P在图4的位置时，写出∠EPF，∠PEB，∠PFD三个角之间的关系并证明（每一步必须注明理由）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上三点A，O，B表示的数分别为6，0，－4，动点P从A出发，以每秒6个单位的速度沿数轴向左匀速运动.
（1）当点P到点A的距离与点P到点B的距离相等时，点P在数轴上表示的数是 ；
（2）另一动点R从B出发，以每秒4个单位的速度沿数轴向左匀速运动，若点P、R同时出发，问点P运动多少时间追上点R？
（3）若M为AP的中点，N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若发生变化，请你说明理由；若不变，请你画出图形，并求出线段MN的长度.
-
科目： 来源： 题型：
查看答案和解析>>【题目】股民李金上星期六买进某公司的股票，每股
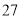元，下表为本周内该股票的涨跌情况：星期
一
二
三
四
五
六
每股涨跌(与前一天相比)
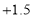
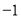
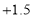
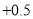
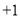
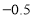
星期三收盘时，每股是________元；本周内最高价是每股________元， 最低价是每股______元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC 中 AB=AC，D、E 两点分别在 AC、BC 上，BD 是∠ABC 的平分线，DE∥AB，若 BE=5cm，CE=3cm，则△CDE 的周长是（ ）
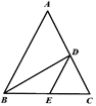
A. 13cmB. 11cmC. 9cmD. 8cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】A，B两地间仅有一长为180千米的平直公路，若甲，乙两车分别从A，B两地同时出发匀速前往B，A两地，乙车速度是甲车速度的
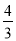倍，乙车比甲车早到45分钟．（1）求甲车速度；
（2）乙车到达A地停留半小时后以来A地时的速度匀速返回B地，甲车到达B地后立即提速匀速返回A地，若乙车返回到B地时甲车距A地不多于30千米，求甲车至少提速多少千米/时？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平整的地面上，10个完全相同的棱长为2cm的小正方体堆成一个几何体．
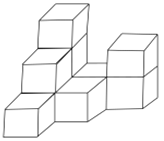
（1）画出从左面看和从上面看的形状图．
（2）如果在这个几何体的表面(不含底面)喷上黄色的漆，这个几何体喷漆的面积是多少cm2．
相关试题
